1.二维向量场

这篇文章介绍了一个平面向量场可视化的网页工具：fieldpaly

这里只是介绍了系统相平面可视化实现的代码，给出了我定义的系统代码标准型，如果对相平面、非线性系统、状态空间、微分方程解的性质等控制的理论内容感兴趣，可以参考我的笔记：相平面法-工程中的数学

从纯数学的角度来讲，这是一个画二维向量场的网站。二维向量场的数学表达：

$$ \boldsymbol{A} = (P,Q) = P(x,y) \cdot \boldsymbol{i} + Q(x,y) \cdot \boldsymbol{j} $$

平面向量场$$ \boldsymbol{A} $$与位置相关，一般纸面上的表达方式是平面上每个点都有一个带箭头的向量。

可视化的表达方式更加直观，通过粒子的运动就能反映向量场的情况。

按照“速度矢量和位置相关”的思路，这个可视化网页提供了一个接口，入口参数为位置，返回参数为该点速度，函数体内可以自己实现数学关系。

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);

  /*  p与v的数学关系实现 */
  
  return v;
}

举个例子，可视化一个点电荷形成的电场。

在原点放置一点电荷带电量为$$ -q $$，试探电荷带电量$$ +q^* $$，其所在位置为$$ \vec r $$

试探电荷受到的力为

$$ \vec F = -k\frac{qq^*}{r^2}\cdot\vec {r^°} $$

则电场强度为

$$ \vec E = \frac{\vec F}{q^*} = -k\frac{q}{r^2}\cdot\vec {r^°} $$

取$$ kq = 1 $$，那么这个电场的表达式为

$$ \vec E = -\frac{\vec {r^°}}{r^2} $$

vec2 get_velocity(vec2 r) {
  vec2 E = vec2(0., 0.);

  E = - （r/length(r)） / (length(r)*length(r));
  
  return E;
}

电场的可视化效果

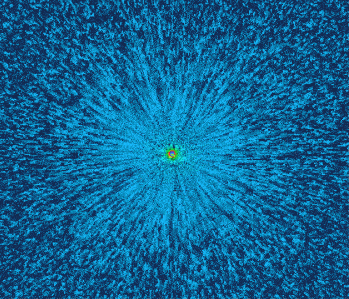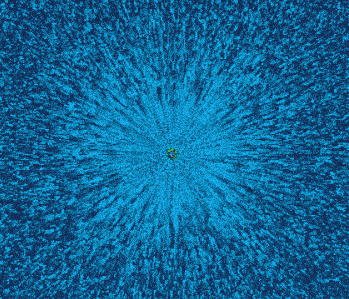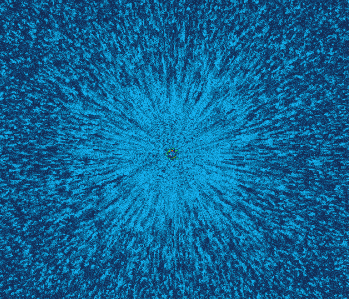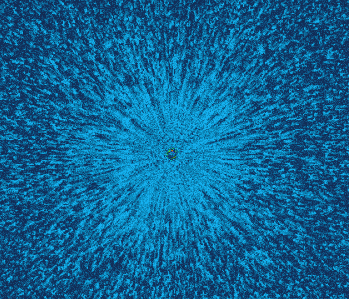
注意这些粒子并不是试探电荷真实的运动，这里的速度是个抽象速度，“速度”反映了场的强度。截屏录制动画的时候不太清晰，实际上还可以通过颜色判断场的强度的。可以看出越靠近中心，强度越高。

这一小段代码使用了函数length()得到向量的模长，此外还有各种数学函数可以使用，以实现各种各样的本质非线性二维场，这为画相平面图提供了很大的帮助，不需要使用if去嵌套实现了。

相平面图在数学上就是个二维向量场，只不过在控制理论里赋予了状态空间的物理意义。因此这个工具完全可以用来画相平面图。系统往往使用状态空间表达式或者微分方程表达的，这里就得考虑怎么用代码实现这两种形式。当然二维平面里只考虑二阶系统。

2.线性系统

2.1线性系统状态空间表达

首先看用状态空间表达式的二阶线性系统。

相平面是不考虑系统输入的，只分析系统在不受控的情况下是怎么运动的。因此状态空间方程就少了输入控制，一个通用表达为：

$$ \left [ \begin{array}{c} \dot{x_1} \
\dot{x_2}
\end{array} \right ] = \left [ \begin{array} {c} a & b \
c & d \end{array} \right ] \left [ \begin{array}{c} x_1 \
x_2
\end{array} \right ] $$

这个形式的状态空间表达式很容易转化成代码，比如说一个具体的系统：

$$ \left [ \begin{array}{c} \dot{x_1} \
\dot{x_2}
\end{array} \right ] = \left [ \begin{array} {c} -3 & 4 \
-2 & 3 \end{array} \right ] \left [ \begin{array}{c} x_1 \
x_2
\end{array} \right ] $$

先判断一下这个系统的特征值为

$$ \mid sI-A \mid = (s+1)(s-1) = 0 $$

根据经典控制理论，有一个在右半平面的极点，因此不稳定，然后看看相轨迹图：

可以看出，是个不稳定的鞍点。代码实现如下，很简单的线性方程组的对应关系，这里参数名用的就是位置和速度，用抽象速度去理解相轨迹也是个很有意思的思路。

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float a,b,c,d;

  a = -3.0;
  b = 4.0;
  c = -2.0;
  d = 3.0;

  v.x = a*p.x + b*p.y;
  v.y = c*p.x + d*p.y;
  
  return v;
}

2.2线性系统微分方程表达

用微分方程或者传递函数表达的线性系统选取合适的状态变量可以很容易的转化成上面的形式。

一个二阶系统

$$ G(s) = \frac{C(s)}{R(s)} = \frac{\omega_n^2}{s^2 + 2\xi\omega_ns+ \omega_n^2} $$

由于研究的是无输入，那么这个系统的微分方程为

$$ \ddot{c} + 2\xi\omega_n\dot{c} + \omega_n^2 c = 0 $$

这里选状态变量$$ x_1 = c, x_2 = \dot{c} $$

那么状态空间表达式为

$$ \left [ \begin{array}{c} \dot{c} \
\ddot{c}
\end{array} \right ] = \left [ \begin{array} {c} 0 & 1 \
-\omega_n^2 & -2\xi\omega_n \end{array} \right ] \left [ \begin{array}{c} c \
\dot{c}
\end{array} \right ] $$

更一般的

对于一个二阶微分方程

$$ \ddot{x} + a\dot{x} + bx = 0 $$

或者系统的特征方程

$$ D(s) = s^2 + as + b = 0 $$

有一个状态空间表达式实现为：

$$ \left [ \begin{array}{c} \dot{x} \
\ddot{x}
\end{array} \right ] = \left [ \begin{array} {c} 0 & 1 \
-b & -a \end{array} \right ] \left [ \begin{array}{c} x \
\dot{x}
\end{array} \right ] $$

实际上这就是可控标准型。

相图的代码实现

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float a,b;

  a = -3.0;
  b = 4.0;

  v.x = p.y;
  v.y = -b*p.x - a*p.y;
  
  return v;
}

3.非本质非线性系统

借助这个思路，来看用微分方程表达的非线性系统。

3.1一个例题

教材上给出的非线性系统的表达为：

$$ \ddot{x} = f(\dot{x},x) $$

由线性系统状态空间表达式代码实现的启发，写成矩阵形式：

$$ \left [ \begin{array}{c} \dot{x} \
\ddot{x}
\end{array} \right ] = \left [ \begin{array} {c} 0 & 1 \
0 & 0 \end{array} \right ] \left [ \begin{array}{c} x \
\dot{x}
\end{array} \right ] + \left [ \begin{array}{c} 0 \
f(\dot{x},x)
\end{array} \right ] $$

举个具体例子，一个系统为

$$ \ddot{x} + 0.5 \dot{x} + 2x + x^2 =0 $$

用代码实现时，写成标准形式：

$$ \ddot{x} = - 0.5 \dot{x} - 2x - x^2 $$

结合矩阵形式，代码实现：

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float x, dot_x, f;
  x     = p.x;
  dot_x = p.y;

  f = -0.5*dot_x - 2.0*x - pow(x,2.0);

  v.x = p.y;
  v.y = f;
  return v;
}

这是胡寿松第六版自动控制原理375页的例题。系统的两个奇点$$ (0,0) $$和$$ (-2,0) $$。

通过稳定点附近线性化可以判断一个是鞍点，一个是稳定焦点。上面的图是精确的相轨迹图。

3.3微分方程表达下的通用代码实现

为了更简单的输入，避免移项负号的问题，就让通式以这个形式出现：

实际上教材里的具体系统基本上也都是这个形式出现的。

我把他叫代码标准型，😂😂，这是我自己下定义起的名字，单纯为了在这里实现可视化效果而写成这种形式。工程上的定义嘛，为了方便使用下的定义也不在少数，所以我也定义一个我觉得不过分。

写成矩阵形式：

$$ \left [ \begin{array}{c} \dot{x} \
\ddot{x}
\end{array} \right ] = \left [ \begin{array} {c} 0 & 1 \
0 & 0 \end{array} \right ] \left [ \begin{array}{c} x \
\dot{x}
\end{array} \right ] - \left [ \begin{array}{c} 0 \
f(\dot{x},x)
\end{array} \right ] $$

通式里面划掉二阶项，$$ \ddot{x} $$，代码里直接实现剩下的部分就可以了。更简单好用。

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float x, dot_x, f;
  x     = p.x;
  dot_x = p.y;

  f = /* f(\dot{x},x) 的代码实现 */;

  v.x = p.y;
  v.y = - f;
  return v;
}

再举几个例子，来自胡寿松习题8-3

$$ \ddot{x} + \dot{x} + \mid x \mid = 0 $$

f = dot_x + abs(x);

$$ \ddot{x} + x + \mathrm{sign} \dot x = 0 $$

f = x + sign(dot_x);

在$$ \dot{x} \ge 0 $$时，有$$ \ddot{x} + x + 1 = 0 $$；在$$ \dot{x} < 0 $$时，有$$ \ddot{x} + x - 1 = 0 $$。

上下平面都是两个椭圆，奇点$$ x_{e1} = -1, x_{e2} = 1 $$。

系统平衡点是一条线，平衡线，或者奇线。

$$ \ddot{x} + \sin x = 0 $$

f = sin(x);

$$ \ddot{x} + 3(\dot x -0.5)\dot x + x + x^2 = 0 $$

f = 3.0*(dot_x - 0.5)*dot_x + x + x*x;

$$ \ddot{x} + x\dot x + x = 0 $$

f = x*dot_x + x ; 

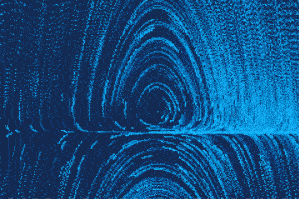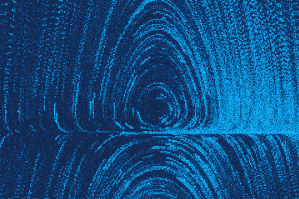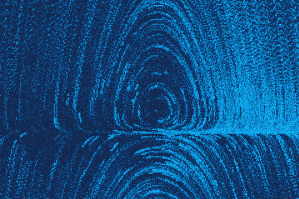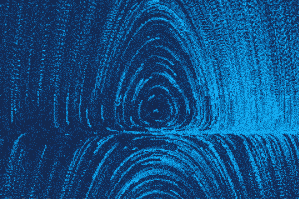
$$ \ddot{x} + \dot x^2 + x = 0 $$

f = dot_x*dot_x + x ;

由上面的举例也可以看出来，有各种各样的数学函数可以使用，更加方便非线性系统的实现，这里列举一些常用的数学函数。

max(,)

log()

sin()

cos()

abs()

length()

exp()

pow()

sign()

本质非线性系统

上面最后提了一下稳定点线性化的事情。这类系统叫非本质非线性系统。线性化以后可以用典型二阶系统看个大概。

还有一类，有典型非线性环节的系统。

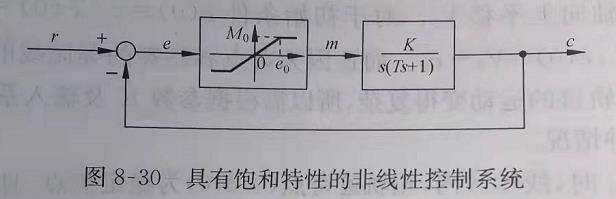
胡寿松第六版377页，系统带有饱和特性。根据信号流向把系统用微分方程写出来，分区画相轨迹，代码实现则是用逻辑语句实现判断

可以对照书上的等倾线法的作图结果

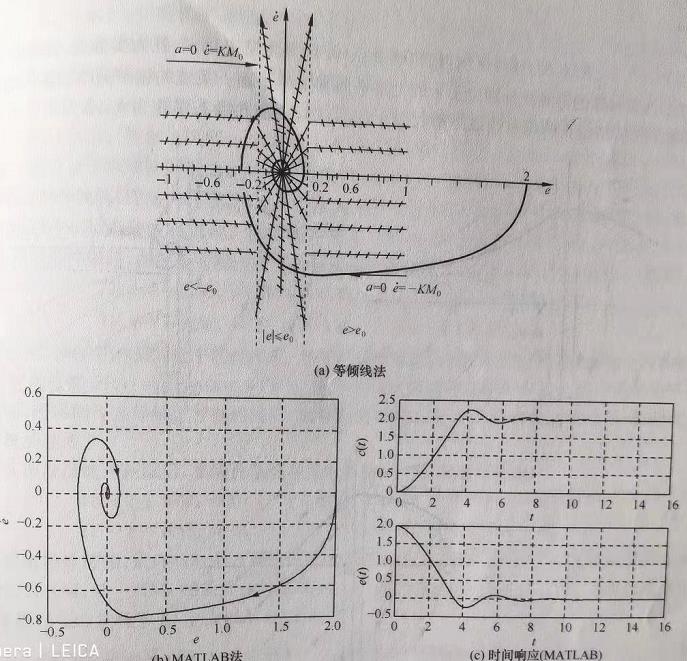
代码实现

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float e,dot_e,f;
  e = p.x;
  dot_e = p.y;

  if (e<=-0.2)
  {
    f = -dot_e + 0.8;
  }
  else if (e>=0.2)
  {
    f = -dot_e - 0.8;
  }
  else
  {
    f = -e - 0.2*dot_e;
  }

  v.x = p.y;
  v.y = f;
  
  return v;
}

再来看一个有滞环环节的非线性系统

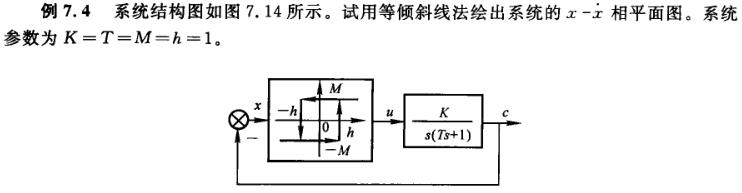
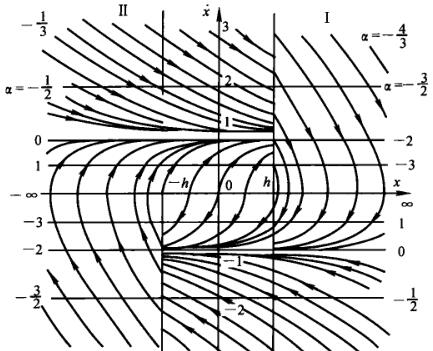
这个不是很好画，手工画的话书上给的是用等倾线法作图。处理出分区表达式以后就可以使用代码实现了：

可以很明显的看到有个极限环，这个系统自由响应的最终结果是自振，这个极限环是稳定的极限环，对于机械系统来说，是可以观察到这种运动的。

对比书上的作图结果

vec2 get_velocity(vec2 p) {
  vec2 v = vec2(0., 0.);
  float c,dot_c,f;
  c = p.x;
  dot_c = p.y;

  if (c<-1.0 || (c<1.0 && dot_c>0.0))
  {
    f = dot_c - 1.0;
  }
  else
  {
    f = dot_c + 1.0;
  }

  v.x = p.y;
  v.y = -f;
  
  return v;
}