转速闭环控制
转速比例控制
根据自动控制原理,将被控量作为反馈量引入系统,与给定量比较,取得偏差进行控制,可以有效抑制扰动造成的影响。
在直流电机控制里,被控量是转速,转速降落是由负载引起的,那么转速反馈闭环可以减小转速降落,从而降低静差率。
比例控制系统结构和静特性
这里把前面的H桥封装起来,输入为VT1和VT4的正脉冲,输出为电机电压
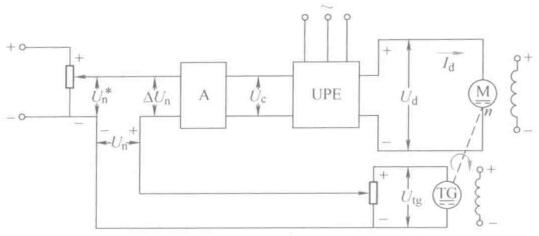
先按照书上这个纯模拟系统分析清楚了,运算放大器前面这两个回路压降相同有
\[U_n^* = \Delta U_n + U_n\]这就实现了计算误差的关系即
\[\Delta U_n = U_n^* - U_n\]比例调节器有
\[U_c = K_P \cdot \Delta U_n\]对后面的PWM变换器,前面开环的时候已经建模过了,有
\[U_d = K_sU_c\]对于电动机,有
\[n = \frac{U_d - I_dR}{C_e \varPhi}\]对于测速发电机
\[U_n = \alpha \cdot n\]数字编码器测速也差不多是这个表达式,所以物理实现不同,但是数学抽象出来是一样的,很猛。
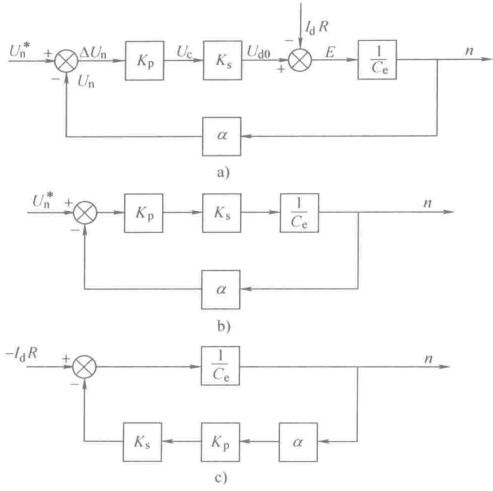
画出来稳态结构框图(a),有两个输入,线性系统叠加原理。用梅森增益公式可以得到总的输出关系式,即为静特性方程式:
\(n = \frac{K_P K_s}{C_e(1+K)}U_n^* - \frac{RI_d}{C_e(1+K)}\)
其中\(K = \frac{K_P K_s \alpha}{C_e}\),实际上是系统的开环增益。
静特性为闭环系统稳定时候电机转速和负载电流(转矩)的关系,形式上和开环机械特性相近,但本质不同。
下面比比哪里不同
开环机械特性和闭环静特性比较
断开反馈回路就是开环系统,开环机械特性就是电压决定转速
\[n = \frac{U_d - I_d R}{ C_e } - \frac{R I_d}{C_e}\]依照前面的,就有了开环理想空载转速\(n_{0open} = \frac{U_d - I_d R}{ C_e }\),开环稳态降速\(\Delta n_{\text{open}} = \frac{R I_d}{C_e}\)
闭环静特性前面已经有了
\[n = \frac{K_P K_s}{C_e(1+K)}U_n^* - \frac{RI_d}{C_e(1+K)}\]同样的,有闭环理想空载转速\(n_{0close} = \frac{K_P K_s}{C_e(1+K)}U_n^*\)和闭环稳态速降\(\Delta n_{\text{close}} = \frac{RI_d}{C_e(1+K)}\)。
同样负载下对比稳态速降,闭环分母多了个\((1+K)\)
\[\Delta n_{\text{open}} = \frac{R I_d}{C_e}\] \[\Delta n_{\text{close}} = \frac{RI_d}{C_e(1+K)}\]K越大,闭环系统的特性越硬。
再来看静差率,按照理想空载转速相同\(n_{0open} = n_{0close}\)来比较,
\[s_{\text{close}} = \frac{\Delta n_{\text{close}}}{n_{0close}}\]很简单的带入,可以发现也是多了个\((1+K)\)
\[s_{\text{close}} = \frac{s_{\text{open}}}{1+K}\]由此简单的量化比较,可以看出闭环系统有更硬的稳态特性,在静差率不变的情况下有更大的调速范围。
闭环系统里,直流电机的额定速降仍然是\(\Delta n_N = \frac{RI_N}{C_e}\),与开环系统的一样,那么闭环系统稳态速降减小的实质是什么呢?
当负载电流增大,电枢压降增大,转速下降,反馈装置感受到了,就提高了PWM变换器输出电压,补偿电阻降落部分影响,电机工作在了一个新的机械特性曲线上,转速又有所回升。闭环系统的静特性是许多开环机械特性各取一个工作点连接而成的。
实质在于自动调节作用,随着负载变化而改变电枢电压,补偿电阻压降。
闭环直流调速系统的反馈控制规律
比例控制的闭环直流调速系统是一种基本的反馈控制系统。反馈控制的基本规律:
- 比例控制开环放大系数\(K\)越大,稳态误差越小,但无法消除
- 反馈控制系统的作用是抵抗扰动(不仅仅负载扰动),除了反馈通道上的都可以
- 系统精度依赖于给定和反馈精度
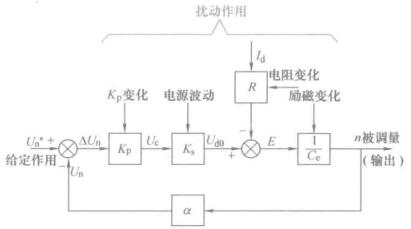
控制系统的作用就是使得输出紧紧跟随给定,并且避免反馈包围内前向通道的干扰。理论讨论的时候只考虑了负载扰动,实际上每个模块都有扰动,但是没关系,反馈系统都可以抑制。在设计闭环系统时,可以只考虑负载扰动,设计好其他扰动也是可以抑制的。
给定作用的微小变化都会使得输出跟随,反馈检测装置的误差也无法通过反馈来克服。因此系统需要有高精度的给定和高精度的反馈。
转速闭环控制的动态性能
比例系数越大,稳态误差越小,这是稳态分析。但是肯定不是越大越好,动态性能制约着比例系数。
动态数学模型
机理分析,写处环节微分方程;求出传奇函数;根据结构画出动态结构框图,求出传奇函数。
前面分析过PWM变换器的近似传递
\[W_s(s) \approx \frac{K_s}{T_s s + 1}\]对于不同的变换器形式都一样,参数有差别。
对于电机
\[U_d = R I_d + L \frac{\text{d} I_d}{\text{d}t} + E\] \[T_e - T_L = \frac{\text{d}\omega}{\text{d}t} = \frac{GD^2}{375} \cdot \frac{\text{d}n}{\text{d}t}\] \[E = C_e n\] \[T_e = C_T I_d\]输入为电压,输出转速,很简单的数学推导有
\[\frac{I_d(s)}{U_d(s) - E(s)} = \frac{1/R}{T_ls + 1}\] \[\frac{E(s)}{I_d(s) - I_{dL}(s)} = \frac{R}{T_ms}\]这里把一些常数性质的参数拿出来用字母简化了,这个简化也是有依据的,不是说为了好看随便搞得。电枢回路时间常数\(T_l = \frac{L}{R}\),机电时间常数\(T_m = \frac{GD^2R}{375C_eC_m}\)
画出来以后,最终目的是得到直流电机的动态传递函数
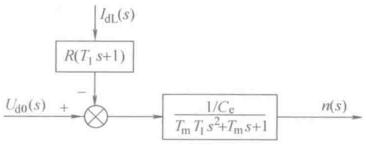
可以看出,额定励磁下的直流电机是一个典型二阶环节,当\(T_m > 4T_l\),过阻尼,如果小于,就是欠阻尼,二阶震荡环节,机械和电磁能量互相转换,电机运动有震荡性质。
点击前面是PWM变换器,一阶系统,此外还有比例控制器,以及测速反馈环节,也是个比例环节,组合起来,就是整个控制系统的结构框图
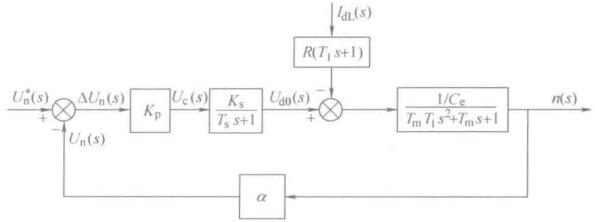
至此,开环传递函数
\[W(s) = \frac{ U_n(s) }{ U_n^*(s) } = \frac{ K }{ (T_s + 1)( T_m T_ls^2 + T_m s + 1 ) }\]闭环函数也可以写出来,但是挺复杂,懒得敲了,很容易写的
\[W_{\text{close}} = \frac{ \frac{K_p K_s}{ C_e(1+K) } }{ \frac{T_m T_l T_s}{1+K}s^3 + \frac{T_m (T_l+ T_s)}{1+K}s^2 + \frac{T_m + T_s}{1+K}s + 1 }\]动态性能的分析
有了传递函数才好做理论分析,\(W_{\text{close}}\)的分母,即特征方程,由劳斯判据,可以知道系统稳定的参数取值
\[K < \frac{T_m}{T_s} + \frac{T_m}{T_l} + \frac{T_s}{T_l}\]转速PI控制
前面的比例控制可以看出,有静差,这里要研究PID控制器,三种作用,先讨论积分控制的作用。
积分控制规律
积分调节器,当输入是转速误差\(\Delta U_n\)时,积分调节器的输入输出关系为
\[U_c = \frac{1}{\tau} \int_0^t \Delta U_n \text{d}t\]传递函数为
\[W_I(s) = \frac{1}{\tau s}\]比例控制是只要电机在工作,就必须有偏差电压,因此这也是有静差的原因。积分调节器只有在静差为0的时候,才停止使输出到一个终值。
比例调节器的输出只取决于输入偏差量的现状,而积分调节器的出书包含了输入偏差量的全部历史。
单独积分控制肯定是不行的,一般都是用比例-积分控制(PI控制)。
传递函数为
\[W_{PI}(s) = K_P + \frac{1}{\tau s} = \frac{K_P \tau s + 1}{\tau s}\]设计PI调节器时候,选择参数也是一个新的问题,在自动控制理论里,有许多方法比如根轨迹法、频域校正等。
转速闭环的小问题
转速反馈把转速作为调节量,检测转速误差,但是如果有个阶跃输入,误差过大,输出拉满,电枢电压过高,这时候相当于全压启动,会造成电机过流。
此外当电机堵转时,也会出现过流问题,反馈控制并不知道堵转了,只是察觉到转速误差一直存在。
这种情况,电流会远远超过允许值,会跳闸或者触发熔断器保护。
因此需要对电流进行一定控制,使得在启动或者堵转时,电流不超过允许值,但是正常运行下又让电流随着负载的增减而变化。
这要求电流负反馈只在制动和堵转时存在,正常运行时消失,这种叫作电流截止负反馈。
模拟实现需要用二极管或者稳压管实现,但是MCU控制简单的if语句就能实现,要简单很多。
有实现方案,这里就不放出来了。因为有更好的方法解决这个问题,就是下一部分内容。
