异步电动机正交坐标系上的动态模型
前面准备工作做好了,左边变换的思路已经有了。
坐标变换可以把三相原始模型简化,按照从特殊到一半,先推导静止两相正交坐标系\(\alpha\beta\),然后推广到旋转正交坐标系\(dq\),运动方程和坐标系没有关系,因此就讨论电压方程、磁链方程、转矩方程。
静止两相坐标系下的动态模型
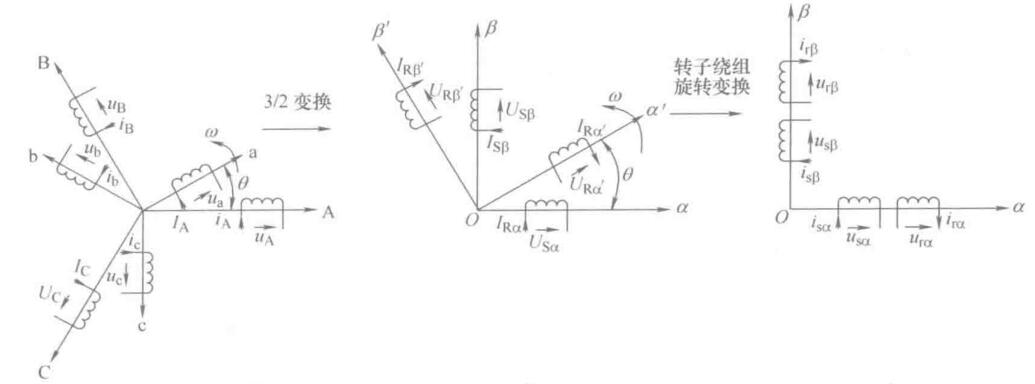
异步电动机定子绕组是静止的,只需要进行3/2变换,转子绕组是旋转的,需要通过3/2变换和旋转到静止的变化,才能变换到静止两相正交坐标系。
定子和转子的3/2变换
对定子三相绕组和旋转的转子三相绕组进行相同的3/2变换,变换后的定子两相正交坐标系\(\alpha\beta\)静止,而转子两相正交坐标系\(\alpha'\beta'\)以角速度\(\omega\)逆时针旋转
原始电压方程
\[\begin{bmatrix} u_A \\ u_B \\ u_C \\ u_a \\ u_b \\ u_c \\ \end{bmatrix} = \begin{bmatrix} R_s& 0 & 0 & 0 & 0 & 0 \\ 0 &R_s& 0 & 0 & 0 & 0 \\ 0 & 0 &R_s& 0 & 0 & 0 \\ 0 & 0 & 0 &R_r& 0 & 0 \\ 0 & 0 & 0 & 0 &R_r& 0 \\ 0 & 0 & 0 & 0 & 0 &R_r\\ \end{bmatrix} \begin{bmatrix} i_A \\ i_B \\ i_C \\ i_a \\ i_b \\ i_c \\ \end{bmatrix} + \frac{\text{d}}{\text{d}t} \begin{bmatrix} \psi_A \\ \psi_B \\ \psi_C \\ \psi_a \\ \psi_b \\ \psi_c \\ \end{bmatrix}\]变换后的电压方程
\[\begin{bmatrix} u_{s\alpha} \\ u_{s\beta} \\ u_{r\alpha'} \\ u_{r\beta'} \\ \end{bmatrix} = \begin{bmatrix} R_s& 0 & 0 & 0 \\ 0 &R_s& 0 & 0 \\ 0 & 0 & R_r& 0 \\ 0 & 0 & 0 &R_r\\ \end{bmatrix} \begin{bmatrix} i_{s\alpha} \\ i_{s\beta} \\ i_{r\alpha'} \\ i_{r\beta'} \\ \end{bmatrix} + \frac{\text{d}}{\text{d}t} \begin{bmatrix} \psi_{s\alpha} \\ \psi_{s\beta} \\ \psi_{r\alpha'} \\ \psi_{r\beta'} \\ \end{bmatrix}\]原始磁链方程
\[\begin{bmatrix} \varPsi_A \\ \varPsi_B \\ \varPsi_C \\ \varPsi_a \\ \varPsi_b \\ \varPsi_c \\ \end{bmatrix} = \begin{bmatrix} L_{AA} & L_{AB} & L_{AC} & L_{Aa} & L_{Ab} & L_{Ac} \\ L_{BA} & L_{BB} & L_{BC} & L_{Ba} & L_{Bb} & L_{Bc} \\ L_{CA} & L_{CB} & L_{CC} & L_{Ca} & L_{Cb} & L_{Cc} \\ L_{aA} & L_{aB} & L_{aC} & L_{aa} & L_{ab} & L_{ac} \\ L_{bA} & L_{bB} & L_{bC} & L_{ba} & L_{bb} & L_{bc} \\ L_{cA} & L_{cB} & L_{cC} & L_{ca} & L_{cb} & L_{cc} \\ \end{bmatrix} \begin{bmatrix} i_A \\ i_B \\ i_C \\ i_a \\ i_b \\ i_c \\ \end{bmatrix}\]变换后磁链方程
\[\begin{bmatrix} \psi_{s\alpha} \\ \psi_{s\beta} \\ \psi_{r\alpha'} \\ \psi_{r\beta'} \\ \end{bmatrix} = \begin{bmatrix} L_{s} & 0 & L_{m}\cos \theta & -L_{m}\sin\theta \\ 0 & L_{s} & L_{m}\sin \theta & L_{m}\cos \theta \\ L_{m}\cos \theta & L_{m}\sin\theta & L_{r} & 0 \\ -L_{m}\sin \theta & L_{m}\cos \theta & 0 & L_{r} \\ \end{bmatrix} \begin{bmatrix} i_{s\alpha} \\ i_{s\beta} \\ i_{r\alpha'} \\ i_{r\beta'} \\ \end{bmatrix}\]变换后的转矩方程:
\[T_e = -n_p L_m [ (i_{s\alpha} i_{r\alpha'} + i_{s\beta} i_{r\beta'})\sin\theta + ( i_{s\alpha} i_{r\beta'} - i_{s\beta} i_{r\alpha'} )\cos\theta ]\]3/2变换把120°分布的三相绕组等效为互相垂直的两相绕组,消除了定子三相绕组之间、转子三相绕组之间的耦合。但是定子绕组和转子绕组之间仍然存在相对运动,因此互感矩阵仍然是一个变参数的非线性矩阵,输出转矩仍然是定转子电流及家教的函数。
3/2变换减少了状态变量的维数,简化了定子和转子的自感矩阵。
静止两相正交坐标系中的矩阵方程

对转子坐标系\(\alpha'\beta'\)做旋转变换(旋转正交坐标系到静止两相正交坐标系的变换),即将\(\alpha'\beta'\)坐标系顺时针旋转\(\theta\),是其与定子\(\alpha\beta\)重合,且保持静止,用静止的两相转子绕组等效代替转动两相绕组。
旋转变换矩阵为
\[\boldsymbol{C_{2r/2s}}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{bmatrix}\]变换后的电压方程为
\[\begin{bmatrix} u_{s\alpha} \\ u_{s\beta} \\ u_{r\alpha} \\ u_{r\beta} \\ \end{bmatrix} = \begin{bmatrix} R_s& 0 & 0 & 0 \\ 0 &R_s& 0 & 0 \\ 0 & 0 & R_r& 0 \\ 0 & 0 & 0 &R_r\\ \end{bmatrix} \begin{bmatrix} i_{s\alpha} \\ i_{s\beta} \\ i_{r\alpha} \\ i_{r\beta} \\ \end{bmatrix} + \frac{\text{d}}{\text{d}t} \begin{bmatrix} \psi_{s\alpha} \\ \psi_{s\beta} \\ \psi_{r\alpha} \\ \psi_{r\beta} \\ \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ \omega\psi_{r\beta} \\ -\omega\psi_{r\alpha} \\ \end{bmatrix}\]磁链方程
\[\begin{bmatrix} \psi_{s\alpha} \\ \psi_{s\beta} \\ \psi_{r\alpha} \\ \psi_{r\beta} \\ \end{bmatrix} = \begin{bmatrix} L_s & 0 & L_m & 0 \\ 0 & L_s & 0 & L_m\ \\ L_m & 0 & L_r & 0 \\ 0 & L_m & 0 & L_r \\ \end{bmatrix} \begin{bmatrix} i_{s\alpha} \\ i_{s\beta} \\ i_{r\alpha} \\ i_{r\beta} \\ \end{bmatrix}\]转矩方程:
\[T_e = n_p L_m ( i_{s\beta}i_{r\alpha} - i_{s\alpha}i_{r\beta} )\]旋转变换改变了定转子之间的耦合关系,消除了定转子绕组夹角对磁链和转矩的影响。
磁链方程是线性定常的方程,但是电压方程中引入了新的非线性因素,还没有改变非线性耦合的性质。
旋转正交坐标系中的动态数学模型
前面是将相对于定子旋转的转子坐标系\(\alpha'\beta'\)做旋转变换,得到了统一的坐标系\(\alpha'\beta'\),这是旋转变换的一个特例。更广义的坐标旋转变换时对定子坐标系\(\alpha\beta\)和转子坐标系同时进行旋转变换,把他们变换到同一个旋转正交坐标系\(dq\)上,\(dq\)坐标系相对于定子的旋转角速度为\(\omega_1\)。
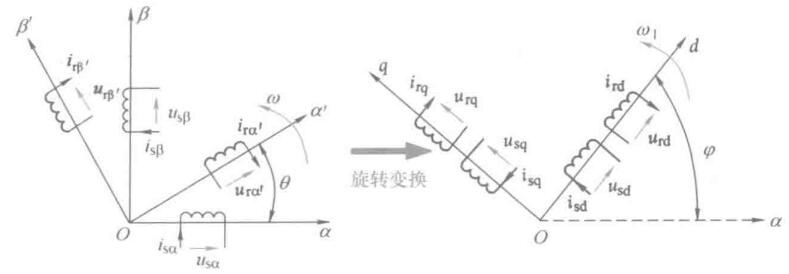
定子的变换矩阵为
\[\boldsymbol{C_{2s/2r}}(\varphi) = \begin{bmatrix} \cos\varphi & \sin\varphi \\ -\sin\varphi & \cos\varphi \\ \end{bmatrix}\]转子的变换矩阵为
\[\boldsymbol{C_{2s/2r}}(\varphi-\theta) = \begin{bmatrix} \cos(\varphi-\theta) & \sin(\varphi-\theta) \\ -\sin(\varphi-\theta) & \cos(\varphi-\theta) \\ \end{bmatrix}\]在\(dq\)坐标系的电压方程为
\[\begin{bmatrix} u_{sd} \\ u_{sq} \\ u_{rd} \\ u_{rq} \\ \end{bmatrix} = \begin{bmatrix} R_s& 0 & 0 & 0 \\ 0 &R_s& 0 & 0 \\ 0 & 0 & R_r& 0 \\ 0 & 0 & 0 &R_r\\ \end{bmatrix} \begin{bmatrix} i_{sd} \\ i_{sq} \\ i_{rd} \\ i_{rq} \\ \end{bmatrix} + \frac{\text{d}}{\text{d}t} \begin{bmatrix} \psi_{sd} \\ \psi_{sq} \\ \psi_{rd} \\ \psi_{rq} \\ \end{bmatrix} + \begin{bmatrix} -\omega_1 \psi_{sq} \\ \omega_1 \psi_{sd} \\ - (\omega_1 - \omega)\psi_{rq} \\ (\omega_1 - \omega)\psi_{rq} \\ \end{bmatrix}\]磁链方程
\[\begin{bmatrix} \psi_{sd} \\ \psi_{sq} \\ \psi_{rd} \\ \psi_{rq} \\ \end{bmatrix} = \begin{bmatrix} L_s & 0 & L_m & 0 \\ 0 & L_s & 0 & L_m\ \\ L_m & 0 & L_r & 0 \\ 0 & L_m & 0 & L_r \\ \end{bmatrix} \begin{bmatrix} i_{sd} \\ i_{sq} \\ i_{rd} \\ i_{rq} \\ \end{bmatrix}\]转矩方程为
\[T_e = n_p L_m ( i_{sq}i_{rd} - i_{sd}i_{rq} )\]旋转变换用旋转绕组代替原来静止的定子绕组,并使等效定子绕组和等效转子绕组重合,并且严格同步,等效后定转子绕组不存在相对运动,所以dq坐标系中的磁链方程和转矩方程与\(\alpha\beta\)坐标系中一样,但是电压方程的非线性耦合更严重了。
表面上看dq坐标系的数学模型还不如\(\alpha\beta\)的,但是其优点是增加了一个输入量\(\omega_1\),为系统控制提供了可能性。磁场定向控制就是通过选择\(\omega_1\)实现的。
旋转速度任意的正交坐标系无实际实用意义,常用的是同步旋转坐标系,将绕组中的交流量变为直流量,模拟直流电动机进行控制。
状态方程
经典控制理论里对于单入单出可以使用传递函数来描述一个系统,前面直流电机控制是基于传递函数在分析。对于交流电机,需要使用现代一点的控制理论了,需要基于状态空间的控制系统分析和设计。首先要已经上述微分和代数方程写处状态空间表达式。
写状态空间表达式的第一个问题是状态变量的选取。旋转正交坐标系(\(dq\)坐标系)上的异步电机有四阶电压方程和一阶运动方程,因此需要选择5个状态变量来描述系统。
可选的状态变量有9个,分为五种:
- 1.转速\(\omega\)
- 2.定子电流\(i_{sd}\)和\(i_{sq}\)
- 3.转子电流\(i_{rd}\)和\(i_{rq}\)
- 4.转子磁链\(\psi_{sd}\)和\(\psi_{sq}\)
- 5.定子磁链\(\psi_{rd}\)和\(\psi_{rq}\)
转速作为输出量必须得选,定子电流可以直接检测到也选。剩下的三组检测就很困难,考虑到磁通恒定一直是我们控制电机很关心的问题,可以在定子磁链和转子磁链任选一组。
这样状态变量的选取就有两种方式
\[\boldsymbol{X} = \begin{bmatrix} \omega \\ \psi_{rd} \\ \psi_{rq} \\ i_{sd} \\ i_{sq} \\ \end{bmatrix}\]或者
\[\boldsymbol{X} = \begin{bmatrix} \omega \\ \psi_{sd} \\ \psi_{sq} \\ i_{sd} \\ i_{sq} \\ \end{bmatrix}\]以\(\omega,i_s,\psi_r\)为状态变量
状态变量
\[\boldsymbol{X} = \begin{bmatrix} \omega \\ \psi_{rd} \\ \psi_{rq} \\ i_{sd} \\ i_{sq} \\ \end{bmatrix}\]输入变量
\[\boldsymbol{U} = \begin{bmatrix} u_{sd} \\ u_{sq} \\ \omega_1 \\ T_L \\ \end{bmatrix}\]输出变量
\[\boldsymbol{Y} = \begin{bmatrix} \omega \\ \psi_r \end{bmatrix}\]经过一系列的操作,整理以后的状态方程为
\[\left.\begin{array}{l} \frac{\mathrm{d} \omega}{\mathrm{d} t}=\frac{n_{\mathrm{p}}^{2} L_{\mathrm{m}}}{J L_{\mathrm{r}}}\left(i_{\mathrm{sq}} \psi_{\mathrm{rd}}-i_{\mathrm{sd}} \psi_{\mathrm{rq}}\right)-\frac{n_{\mathrm{p}}}{J} T_{\mathrm{L}} \\ \frac{\mathrm{d} \psi_{\mathrm{rd}}}{\mathrm{d} t}=-\frac{1}{T_{\mathrm{r}}} \psi_{\mathrm{rd}}+\left(\omega_{1}-\omega\right) \psi_{\mathrm{rq}}+\frac{L_{\mathrm{m}}}{T_{\mathrm{r}}} i_{\mathrm{sd}} \\ \frac{\mathrm{d} \psi_{\mathrm{rq}}}{\mathrm{d} t}=-\frac{1}{T_{\mathrm{r}}} \psi_{\mathrm{rq}}-\left(\omega_{1}-\omega\right) \psi_{\mathrm{rd}}+\frac{L_{\mathrm{m}}}{T_{\mathrm{r}}} i_{\mathrm{sq}} \\ \frac{\mathrm{d} i_{\mathrm{sd}}}{\mathrm{d} t}=\frac{L_{\mathrm{m}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}} T_{\mathrm{r}}} \psi_{\mathrm{rd}}+\frac{L_{\mathrm{m}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}} \omega \psi_{\mathrm{rq}}-\frac{R_{\mathrm{s}} L_{\mathrm{r}}^{2}+R_{\mathrm{r}} L_{\mathrm{m}}^{2}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}^{2}} i_{\mathrm{sd}}+\omega_{1} i_{\mathrm{sq}}+\frac{u_{\mathrm{sd}}}{\sigma L_{\mathrm{s}}} \\ \frac{\mathrm{d} i_{\mathrm{sq}}}{\mathrm{d} t}=\frac{L_{\mathrm{m}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}} T_{\mathrm{r}}} \psi_{\mathrm{rq}}-\frac{L_{\mathrm{m}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}} \omega \psi_{\mathrm{rd}}-\frac{R_{\mathrm{s}} L_{\mathrm{r}}^{2}+R_{\mathrm{r}} L_{\mathrm{m}}^{2}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}^{2}} i_{\mathrm{sq}}-\omega_{1} i_{\mathrm{sd}}+\frac{u_{\mathrm{sq}}}{\sigma L_{\mathrm{s}}} \end{array}\right\}\]其中,电动机漏磁系数\(\sigma = 1 - \frac{L_m^2}{L_sL_r}\),转子电磁时间常数\(T_r = \frac{L_r}{R_r}\)
输出方程
\[\boldsymbol{Y} = \begin{bmatrix} \omega \\ \sqrt{\psi_{rd}^2 + \psi_{rq}^2} \end{bmatrix}\]以\(\omega,i_s,\psi_s\)为状态变量
状态变量
\[\boldsymbol{X} = \begin{bmatrix} \omega \\ \psi_{sd} \\ \psi_{sq} \\ i_{sd} \\ i_{sq} \\ \end{bmatrix}\]输入变量
\[\boldsymbol{U} = \begin{bmatrix} u_{sd} \\ u_{sq} \\ \omega_1 \\ T_L \\ \end{bmatrix}\]输出变量
\[\boldsymbol{Y} = \begin{bmatrix} \omega \\ \psi_s \end{bmatrix}\]经过操作以后
\[\left.\begin{array}{l} \frac{\mathrm{d} \omega}{\mathrm{d} t}=\frac{n_{\mathrm{p}}^{2}}{J}\left(i_{\mathrm{sq}} \psi_{\mathrm{sd}}-i_{\mathrm{sd}} \psi_{\mathrm{sq}}\right)-\frac{n_{\mathrm{p}}}{J} T_{\mathrm{L}} \\ \frac{\mathrm{d} \psi_{\mathrm{sd}}}{\mathrm{d} t}=-R_{\mathrm{s}} i_{\mathrm{sd}}+\omega_{1} \psi_{\mathrm{sq}}+u_{\mathrm{sd}} \\ \frac{\mathrm{d} \psi_{\mathrm{sq}}}{\mathrm{d} t}=-R_{\mathrm{s}} i_{\mathrm{sq}}-\omega_{1} \psi_{\mathrm{sd}}+u_{\mathrm{sq}} \\ \frac{\mathrm{d} i_{\mathrm{sd}}}{\mathrm{d} t}=\frac{1}{\sigma L_{\mathrm{s}} T_{\mathrm{r}}} \psi_{\mathrm{sd}}+\frac{1}{\sigma L_{\mathrm{s}}} \omega \psi_{\mathrm{sq}}-\frac{R_{\mathrm{s}} L_{\mathrm{r}}+R_{\mathrm{r}} L_{\mathrm{s}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}} i_{\mathrm{sd}}+\left(\omega_{1}-\omega\right) i_{\mathrm{sq}}+\frac{u_{\mathrm{sd}}}{\sigma L_{\mathrm{s}}} \\ \frac{\mathrm{d} i_{\mathrm{sq}}}{\mathrm{d} t}=\frac{1}{\sigma L_{\mathrm{s}} T_{\mathrm{r}}} \psi_{\mathrm{sq}}-\frac{1}{\sigma L_{\mathrm{s}}} \omega \psi_{\mathrm{sd}}-\frac{R_{\mathrm{s}} L_{\mathrm{r}}+R_{\mathrm{r}} L_{\mathrm{s}}}{\sigma L_{\mathrm{s}} L_{\mathrm{r}}} i_{\mathrm{sq}}-\left(\omega_{1}-\omega\right) i_{\mathrm{sd}}+\frac{u_{\mathrm{sq}}}{\sigma L_{\mathrm{s}}} \end{array}\right\}\]输出方程
\[\boldsymbol{Y} = \begin{bmatrix} \omega \\ \sqrt{\psi_{sd}^2 + \psi_{sq}^2} \end{bmatrix}\]