异步电机稳态数学模型
稳态数学模型
稳态等效电路
稳态数学模型:稳态等效电路,机械特性。
稳态等效电路描述了一定转差率下电动机的稳态电气特性;机械特性描述了转矩与转差率(转速)的稳态关系。
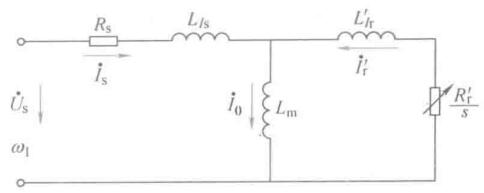
根据电机学原理,稳定模型可以用T形等效电路表示
按照定义,转差率和转速的关系
\[s = \frac{n_1 - n}{n_1}\]其中,同步转速\(n_1 = \frac{60f_1}{n_p}\),电源频率\(f_1\),电动机极对数\(n_p\)
等效电路图里,\(R_s, R_r'\)定子每相绕组电阻、折合到定子侧的转子每相绕组电阻;\(L_{ls}, L_{lr}'\)定子每相漏感、折合到定子侧的每相转子漏感;\(L_m\)定子每相绕组产生的气隙主磁通等效电感,励磁电感;定子相电压\(\dot U_s\);对于电流,箭头为规定方向。
由等效图可以导出转子相电流幅值,表达式挺复杂,但是就是一个简单的复阻抗计算。一般情况下,\(L_m >> L_{ls}\),从表达式上来看,相当于没有\(L_m\)
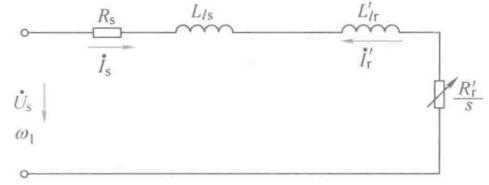
由此简化等效电路,可以得出电流幅值公式(计算机械特性会用到):
\[I_s \approx I_r' = \frac{U_s}{ \sqrt{ \left( R_s + \frac{R_r'}{s} \right)^2 + \omega_1^2 (L_{ls} + L_{lr}')^2 } }\]这里实际上是电机学要解决的问题,可以参考前面电机学内容。
电机内部的理论是电磁场问题。本质是场,但是可以使用路来分析。磁场的分析也可以简化为磁路的分析。然后把电路和磁路又简化为单一电路问题,即归算后的等效电路、方程式和相量图。
整个研究思路:
电机电磁场问题👉电路、磁路👉归算为电路,方程式,相量图👉归算到定子侧单一电路
因此可以看到,等效电路都是连起来的,而实际电机我们知道,转子和定子并无电上的直接联系,通过气隙磁场传递能量。
机械特性
和前面直流电机机械特性一样,指的是机械量之间的关系,即转速\(n\)和转矩\(T_e\)之间的关系。对于异步电动机来讲,转速和转差率是等价的。
三相异步电机传递的电磁功率为
\[P_m = 3\cdot I_r'^2 \frac{ R_r'}{ s }\]机械同步角速度为
\[\omega_{m1} = \frac{\omega_1}{n_p}\]则异步电机的电磁转矩为
\[T_e = \frac{P_m}{\omega_{m1} } = \frac{ 3n_p U_s^2 R_r'/s }{\omega_1 \left[ \left( R_s + \frac{R_r'}{s} \right)^2 + \omega_1^2 ( L_{ls} + L_{lr}' )^2 \right]}\]进一步整理的好看一点就是机械特性方程,表征了转矩和转差率的关系:
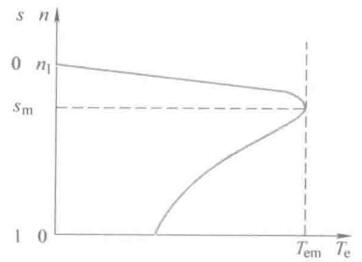
\[T_e = \frac{ 3n_p U_s^2 R_r's }{\omega_1 \left[ \left( s R_s + R_r' \right)^2 + s^2 \omega_1^2 ( L_{ls} + L_{lr}' )^2 \right]}\]虽说好看,但是还是有点难看的😂,倒是思路并不困难。和直流电机一样,我们想得到\(T_e -s\)曲线,这就是一个数学上已知表达式画图的问题了,求极值、增减性、凹凸性、拐点、渐近线等等方法都可以用上了(从会的工具里挑几个能在这里用上的)。
对变量\(s\)求导,\(\frac{\text{d}T_e}{\text{d}s} = 0\),可以找到最大转矩\(T_{em}\)对应的转差率\(s_m\),机械特性是有这个特殊点存在的。
临界转差率
\[s_m = \frac{R_r'}{\sqrt{R_s^2 + \omega_1^2( L_{ls} + L_{lr}' )^2}}\]临界转矩
\[T_{em} = \frac{3n_p U_s^2}{2\omega_1[R_s + \sqrt{R_s^2 + \omega_1^2( L_{ls} + L_{lr}' )^2} ]}\]这里用近似分析思想,分母展开,s比较小时(同步转速附近),忽略分母含s的各项有
\[T_e \approx \frac{3n_p U_s^2 R_r's}{ \omega_1 R_r'}\]这段为直线。
在s较大时,分母中\(s^2\)对函数值起主导作用,有
\[T_e \approx \frac{3n_p U_s^2 R_r's}{\omega_1 s [ R_s^2 + \omega_1^2( L_{ls} + L_{lr}' )^2 ]}\]转差率比较大时候,接近反比例关系。
由额定电压\(U_{sN}\)、额定频率\(f_{1N}\)供电,时候的机械特性方程为固有特性或自然特性:
\[T_e = \frac{ 3n_p U_{sN}^2 R_r's }{\omega_{1N} \left[ \left( s R_s + R_r' \right)^2 + s^2 \omega_{1N}^2 ( L_{ls} + L_{lr}' )^2 \right]}\]调速方法
调速就是认为改变机械特性参数,使电机的稳定工作点偏离固有机械特性,工作在人为机械特性上。
由机械特性方程可知可以改变的参数有电机参数、电源电压\(U_s\)、电源频率\(f_1\)。
这里着重研究改变电压调速和改变频率调速。
三相异步电动机定子每相电动势的有效值为
\[E_g = 4.44 f_1 N_s k_{N_s} \varPhi_m\]其中,\(E_g\)气隙磁通在定子侧每相感应电动势的有效值;\(N_s\)定子绕组串联匝数;\(k_{N_s}\)定子基波绕组系数;\(\varPhi_m\)每极气隙磁通量。
如果忽略定子绕组电阻和漏磁感抗压降,可认为定子相电压\(U_s \approx E_g = 4.44 f_1 N_s k_{N_s} \varPhi_m\)
则气隙磁通\(\varPhi_m\)是由\(U_s\)决定的,在调速的过程中,应当保持气隙磁通不变化,即
\[\frac{E_g}{f_1} = \text{Constant}\]或者近似认为
\[\frac{U_s}{f_1} = \text{Constant}\]