定积分与微分
定积分
去考虑圆的面积公式,尝试用圆环叠加去近似,同样的更数学化的例子是算一个坐标系中不规则图形的面积,使用矩形去近似。更实际的例子是知道车辆速度去求行驶距离。这些问题都会等价到最后求曲边梯形的面积,这就是数学中的抽象思维。将事物的共同点提取出来,就是求大量的很小的东西加起来。
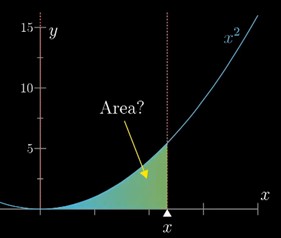
那么这个问题又该怎么解决呢?继续做问题的等价:把左端点固定,让右端点移动,能不能找到一个函数A(x)代表抛物线下的面积。一个巧妙的思考方法:如果x增加一小点dx,那么面积增加量dA近似等于x^2dx,增加量越小越准确。也就是说dA/dx≈x^2,对于更一般的函数有dA/dx≈f(x),这里又遇到了另一个重要概念:导数。问题又被等价成了能不能找到一个函数的导数是f(x)。从这个角度可以引出导数、微分方程的概念。
(3B1B视频)
定积分的定义
\[S = \lim_{\lambda \to 0} \sum_{i=1}^n f(\xi_i) \Delta x\]求曲边梯形可以归结上求这种类型的极限。
这个极限记作
\[I = \int_a^b f(x)dx\]不管怎么取,这个极限值是相同的,但是有种特殊的取法
\[\lim_{n \to \infty} \sum_{i=1}^n f(0 + \frac{x-0}{n}i)\frac{x-0}{n} = \int_0^xf(t)dt\]数列求和,转换成积分问题来解决。
微分
3B1B笔记
从定积分开始
导数的悖论
导数通常描述为瞬时变化率,其实仔细思考这个说法是矛盾的,拍一张车辆运动的照片,这是一个瞬间,能看出速度吗?显然不太行。那么速度到底是什么,速度的来源是距离/时间,即∆x/∆t,这是速度的本质,也就是说要是速度一定得有时间的变化,那这个速度还是瞬时速度吗?
因此有了数学上的dt,这个dt是个无限接近0的东西但是不是0,,听起来更像是在狡辩。但是这个想法很巧妙的绕开了瞬时和变化的关系,这个东西巧妙的描述了瞬间的变化,辩证统一。
以一个函数f(x)=x^3为例子求导数
\[f'(x) = \frac{f(x+dt)-f(x)}{dt} = \frac{(x+dt)^3-x^3}{dt} = 3x^2 dt+[3x(dt)]^2+(dt)^3/dt=3x^2+3xdt+(dt)^3\]这个计算过程没有出现lim的运算但是又处处体现的极限的思想,因为dt本身就是一个极限(无穷小)。同时这个结果也表达了微分的含义,同时也可以看到级数的身影。
接着这个特殊函数去思考,若f是车的位置,那么在t=0时刻,车子在动吗?如果t=0时刻车没动,那么车又是什么时候开始动的呢?这就是前面那个悖论,这个问题实际上是没有意义的,问题是基于一个不存在的概念"瞬时变化",而导数不是用来测量"瞬时变化的",导数为0的含义是:当时间的间隔变得越来越小时,这个表示速度的比值就越趋近于0。这不是说车是静止的,是说他此时运动速度近似于0。瞬时变化率的准确含义是"变化率的最佳近似"。(实际上又回到了∆y/∆x)
工程应用需要理解这些数学表达是在描述什么,至于计算的问题,给出表达式交给数学家去算,他们会给我们纯数学的解学方案。
极限
前面不经意间提到了极限这个名词,极限看起来是一个直觉的想象概念,但是数学上确给了严谨的定义。再来看导数的定义:
(lim)┬(∆x→0)〖(f(x+∆x)-f(x))/∆x〗
这是导数的标准定义式,和前面不同没用dt,因为d本身就代表了趋近的意思。 极限存在,收缩x,f(x)是一个确定值。
再来看看洛必达法则,洛必达实际上想表达这么个事情,只不过吧dx约掉了,实际上是泰勒展开后的特殊情况,也体现了微分中以直带曲在极限过程中精确的思想。
(lim)┬(x→x_0 )〖(f(x_0))/(g(x_0))=(lim)┬(x→x_0 )〖(f'(x)dx)/(g'(x)dx)〗 〗
积分
想象闭着眼坐在车里,凭感觉判断车走了多远,这是一个粗略的惯性导航,有一些应用也是这么干的,间隔时间用传感器测加速度,将加速度累加得到速度。这个问题在第一部分粗略的谈过,抽象成了求曲边梯形的面积。这个运算恰好是第二部分导数中的逆运算。 在没有讲极限之前,这个问题可能比较困难,只能用矩阵面积和近似替代,在实际的机器人离散系统里也是这么做的,所以会有积分累加误差。矩形面积越小越精确,很自然的想到"极限"情况下就是等于的。
自己写的
一元微分
经典控制理论的研究对象是微分方程,但是在工程应用经典控制理论的分析方法时,先需要有这么一个微分方程,实际上显示被控对象几乎都是非线性的,这时候就需要做一个线性化处理。线性化处理的数学理论基础就是这一部分。一些相似的思想:微分以直代曲、无穷小等价、级数展开更高阶的近似,更抽象的可以用线性代数的抽象空间来理解,实际上图像压缩算法里也蕴含着这种抓主要特征、忽略高阶项的思想。
这里先以以直代曲作为切入点,整理一元微分学的重要知识点。
可微和极限
高中物理学简谐运动的时候有个经典的单摆实验。最终得出的结论是单摆运动周期T仅与摆长l有关系,摆长越长,周期越大\(T = 2\pi \sqrt{\frac{l}{g}}\)
在进行力学分析时有一个重要的近似:在\(\theta \le 5 \degree\)即平衡点附近\(sin\theta \approx \theta \approx \frac{x}{l}\)
可微、极限、导数
连续和可导
分析学性质
做题的东西
中值定理
工程物理上的应用
工程应用
