统计基础
概率应用到实际。
统计学更细致的研究事情之间的关系,一个典型的,疫苗的临床试验。实验组与对照组。
根据实验得到的数据,来研究随机现象,对研究对象的客观规律做出合理的估计和判断。
前面概率理论里随机变量的分布都是已经知道的,在知道分布的情况下研究分布的规律。
在统计里,随机变量的分布并不知道,所以需要进行实验观测,来推断分布。所以第一步就是实验了
样本与抽样分布
统计量
\(X\)有分布函数\(F\),当然我们不知道F,但是F是客观存在的。做n次实验,那么就得到了一个容量为n的简单随机样本\(X_1,X_2,\cdots,X_n\),这n个实验做完了,每个实验都有个具体值,这n个值就是样本值\(x_1,x_2,\cdots,x_n\)
一个随机变量有分布函数和概率密度,一个样本也有分布函数和概率密度。
样本\((X_1,X_2,\cdots,X_n)\)的分布函数为
\[F^*(x_1,x_2,\cdots,x_n) = \prod _{i=1}^n F(x_i)\]这也很合理,因为每次实验是独立的。
同样的样本的概率密度
\[f^*(x_1,x_2,\cdots,x_n) = \prod _{i=1}^n f(x_i)\]可以看出来有了这两个东西,一个样本\((X_1,X_2,\cdots,X_n)\)和一个随机变量就有点像了,确实研究样本也是用随机变量取研究的,只不过是把一个样本构造成函数\(g(X_1,X_2,\cdots,X_n)\)。
\(g(X_1,X_2,\cdots,X_n)\)这个随机变量就起个新名字叫统计量了。同样的可以算统计量的数字特征,这在后面会有充分的应用。
常用的样本函数(统计量)有以下这几个
样本平均值
\[\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i\]样本方差
\[S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2 = \frac{1}{n-1} \left(\sum_{i=1}^n X_i^2 - n\overline{X}^2 \right)\]随机变量函数并不是新东西了。
概率分布里面,比较麻烦的那几类计算题,就是随机变量函数的分布,只不过最多研究到了二元函数,到这里维数变多了。
这里还是要再次准确理解一下随机变量,和随机变量的值这个事情。样本均值和生活里常说的平均值以及数学上讲的期望是两回事。
生活里常讲的平均值,比如说一个班的高考平均成绩,是高考考完试了,分数都公布了,分数的平均值。实际上是一次实验的结果。
期望不依赖一次具体实验,实际上这个顺序都不对,应该是具体实验反映客观存在的期望。谁先谁后要摆对位置。高考之前成绩期望在上帝视角来看就是有的。
统计量,比如样本均值,是个随机变量,有点像EXCEL的一个公式的运算法则,统计量是一个个空格的运算求和方法,填入数据之前,这个法则就存在了,但是每个格子的值在填进去之前是不知道的。
每次实验都会有一组具体数据,比如样本均值,每次月考是一次实验,使用这个法则能算出一个具体的数字,即统计量的值,这个值一定程度上可以反映期望的。模拟次数越多,一个班学生的做题水平(期望)越能得到充分的反映。
大概就是这么个意思,再往后大数定律都要出来了😂,无穷次考试直接毕竟一个班的做题真实水平。实际上这是不准确的,有点混淆一堆学生和一个班关系了,这有点像是统计量的统计量,我也不知道我再说啥,已经晕了。后面清醒了再完善这里的表述吧。。。
每次实验的结果,即统计量的观察值
\[\overline{x} = \frac{1}{n}\sum_{i=1}^n x_i\]样本方差
\[s^2 = \frac{1}{n-1}\sum_{i=1}^n (x_i - \overline{x})^2\]我觉得学统计一定要搞明白符号背后的含义,数学符号是在讲事情的。符号代表了背后的客观事情的。
不然这观察值和统计量,这一看,这不就大写换小写嘛😂😂😂😂。这有啥区别。
这可区别大了,小写的意思是高考都考完了,成绩都出来了。大写代表的是一个无法具体量化的做题能力,就这么理解吧,感觉这么说也不准确,但是还是有点道理的。成绩在我能力上下波动,很合理。
其实不仅仅是统计学,应用数学都是在用数学符号讲一个客观事情的。如果搞懂了数学背后客观世界的事情,那么数学符号这一种人创造的主观表达就会显得合理精妙简约有力。
这让我不仅又想到了什么是辩证法,以及辩证唯物论,学数学就是在脑内建立对客观世界的映像的过程。而符号传达的信息有限,符号一旦写下就已经有了和符号代表的事物本身的割裂,这是上面未名子辩证法的东西,所以找到数学符号代表的实际在讲的事情,会对数学有更深刻的理解。
数学有个很恐怖的地方,既使没法把数学和数学描述的客观世界做到辩证统一,基于数学体系的底层严密定义,各种上层定理推论也是自洽的。我觉得这也是造成会做数学题和懂数学割裂开的原因。
。。。又跑题了。。。
统计量的分布
统计量\(g(X_1,X_2,\cdots,X_n)\)是随机变量,自然也就有分布函数概率密度数字特征了。
统计量的分布叫抽样分布,几个来自正态总体的常用的统计量的分布
- \(\chi^2\)分布
\(X_i \sim N(0,1)\),注意是标准正态分布
\[\chi^2 = X_1^2 + X_2^2 + \cdots X_n^2\]服从自由度为n的\(\chi^2\)分布,记为\(\chi^2 \sim \chi^2(n)\)
\[E(\chi^2) = n , D(\chi^2) = 2n\]- \(t\)分布
\(X \sim N(0,1),Y \sim \chi^2(n)\),并且\(X,Y\)相互独立,那么随机变量
\[t = \frac{X}{\sqrt{Y/n}}\]服从自由度为n的t分布,记为\(t \sim t(n)\)
- \(F\)分布
- 正态总体的样本均值和样本方差的分布
首先不管是什么分布,都有
\[\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i\] \[S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2 = \frac{1}{n-1} \left(\sum_{i=1}^n X_i^2 - n\overline{X}^2 \right)\]这两个统计量的数字特征
\[E(\overline{X}) = \mu, D(\overline{X}) = \frac{\sigma^2}{n}\] \[E(S^2) = \sigma^2\]然后考虑样本是正态分布下的情况。
因为独立同分布,所以加起来也服从正态分布。即样本均值也服从正态分布
\[\overline{X} \sim N(\mu, \sigma^2/n)\]样本方差的分布
\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\]并且\(\overline{X}\)与\(S^2\)独立
对于样本均值有了正态,那么标准化一下
\[\frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim N(0, 1)\]更多的时候,方差也不知道,那么就用样本方差,这时候不是标准正态分布了,是t分布,虽然稍微差了点,但是好歹有。
\[\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)\]这几个分布是干啥用的呢?看后面区间估计和假设检验。
参数估计
用实验来判断分布,是统计要解决的问题。其中一类就是估计问题,另一类是下一个部分,假设检验问题。
点估计
分布形式知道了,但是有个参数不知道,但是做了一堆试验能不能从实验推测出参数的问题。
对于一个样本\((X_1,X_2,\cdots,X_n)\),实验的样本值\((x_1,x_2,\cdots,x_n)\)
一阶矩估计
\[\overline X = EX\]让实验值和理论值相等,强行算出一个可能的参数值。
算出来的是我觉得参数最有可能的值
二阶矩估计
\[\frac{1}{n}\sum_{i=1}^n X_i^2 = EX^2\]最大似然估计
取到这个样本的这组值发生的概率为
\[L(x_1,x_2,\cdots,x_n) = \prod _{i=1}^n f(x_i,\theta)\]取到这组值了,说明取这值的概率挺大的,就是个极值问题了。
举例子
设总体X的概率密度为\(f(x) = \frac{1}{2\theta} e ^ {-\frac{\mid x \mid}{\theta}}\)
\(X_1, X_2 , \dots , X_n\)是取自X的样本,求矩估计和最大似然估计。
估计量的评价
估计的好不好呢。也是个数字特征,指标的问题。
无偏性
\[E(\hat{\theta}) = \theta\]有效性
\[E(\hat{\theta}_1) = E(\hat{\theta}_2) = \theta\] \[D(\hat{\theta}_1) < D(\hat{\theta}_2)\]一致性,相合性
\[\lim_{n \to \infty}P\{ \mid \hat{\theta} - \theta \mid < \varepsilon \} = 1\]区间估计
均值和期望有啥关系呢?没啥关系。但是不全没有。
比如我的做题能力用分数来衡量的话是个客观值\(EX = \mu\),每次考试都是一次实验\(X_i\),考试成绩可是有高有低的,这就说期望和单次实验不等,没啥关系。但是成绩也是在一定范围内波动的,不能说我数学学的好(能力高),一次考90,一次考20(概率极小)。也就是说,考试次数足够多,是可以比较准确的反映做题能力的。
能力强但是考的成绩太低是个小概率事件,这个事情的数学描述
\[P \{ \mid \overline X - \mu \mid > \Delta ) < \alpha\]这里α是显著性水平,1-α叫作置信度。也就是说我实验做出来的样本均值过分的偏离期望。
实际上\(\alpha\)是个小概率的意思,往往表示不希望发生。
每次考试会因为出题难度,身体状态,成绩有波动,就认为是在正态总体下\(X_i \sim N(\mu, \sigma^2)\)。如果不是正态,有中心极限定理。
一般研究正态的东西都会标准化后操作
\[P \left( \left | \frac{\overline X - \mu}{\sigma/\sqrt{n}} \right | > z_{\frac{\alpha}{2}} \right) = \alpha\]使用多次考试的平均值,去衡量客观做题能力。即能力离开平均成绩太远是个小概率事件。那么反过来是不是可以说,能力不会离开平均成绩太远,做题能力在一个分数范围内。这就是用区间去估计能力。
\[P \left( \left | \frac{\overline X - \mu}{\sigma/\sqrt{n}} \right | < z_{\frac{\alpha}{2}} \right) = 1 - \alpha\]看概率密度分布图,用上α分位点的定义,拎出来
\[P \left( \overline X - \frac{\sigma}{\sqrt{n}}z_{\alpha/2} < \mu < \overline X + \frac{\sigma}{\sqrt{n}}z_{\alpha/2} \right ) = 1 - \alpha\]多次考试的平均成绩,做题能力不会离开这个平均成绩太远,我们有\(1 - \alpha\)的把握说这个事绝对没问题。
也就说我估摸着期望落在一个区间里的概率足够大。
这个区间就被叫做了置信水平为α的置信区间
\[\left ( \overline X - \frac{\sigma}{\sqrt{n}}z_{\alpha/2} , \overline X + \frac{\sigma}{\sqrt{n}}z_{\alpha/2} \right)\]可是σ也不知道,那么没关系,使用样本方差
那么退一步,样本方差是可以算出来的,也就是我多次考试的成绩波动。就用这个样本方差
\[\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)\]这时候就是t分布,虽然不如标准正态那么优秀,但是也总是能用的。
\[P \left( \left | \frac{\overline X - \mu}{S/\sqrt{n}} \right | < t_{\frac{\alpha}{2}}(n-1) \right) = 1 - \alpha\]思路还是一样的,能力又落在平均成绩附近的一个范围内了。
现在应该理解的差不多了。更数学一点,估计方差。
\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\]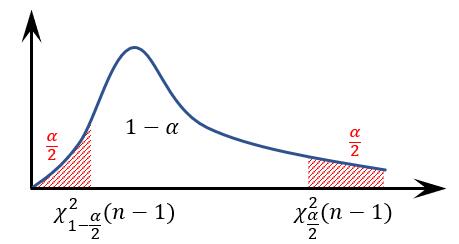
解出来,那么这个区间就又有了
这里也能看出,上面的统计量的分布在这里全部都是有用的。
假设检验
假设检验,又是咋回事呢。
接着前面,α是小概率事件,比如我假设,我的做题能力相当差。最后发现离平均值过远,落到了α的范围内,那么,说明假设就是不对的。
拒绝\(H_0\)
