离散系统基础
理想采样函数联系起了连续信号和离散信号。
对于离散信号,我们用频谱分析得出采样后还原连续信号的条件,这就是香农定理。
然后我们再对采样连续信号进行拉普拉斯变换,进行的个代换起个名字叫z变换。
这个变换的地位再离散系统里个拉普拉斯的地位是一样的,提供了一个在复频域的视角。
离散系统和离散信号
离散系统指的是系统里面一处或几处是脉冲串或者数码。
离散系统有采样系统和数字系统。采样系统是实践离散但是数值连续,数字系统的数值也离散了,比如8bit只能表示0-255的整数,在值上也有量化误差。
用编程实现控制有相当多的好处,能程序实现各种算法,所有的控制器比如超前滞后啥的没有硬件电路了,全都用编程实现。此外还能联网,很强。
当然也有采样点间信息丢失的问题,和相同条件的连续系统相比,性能会有所下降(后面会用数学推)。此外还得要A/D以及D/A装置。
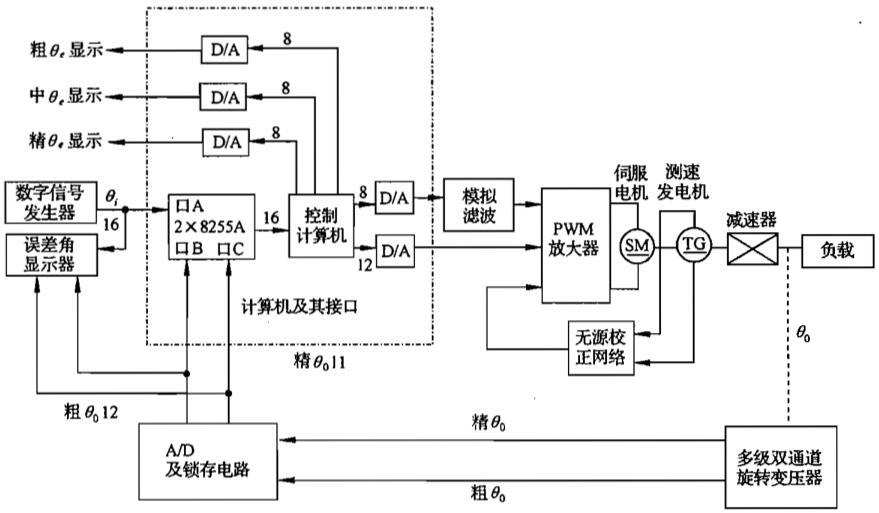
比如上面就是个书上举的例子。小口径高炮高精度伺服系统,最终是要控制转角,是个电机相关的控制系统。可以看出来比较老了,8255A作为IO口,可能控制计算机是8088这个时代的东西。
这个实际的系统大概画出来这这个样子的,这个框图不是数学上的框图,需要想办法用数学语言描述出来
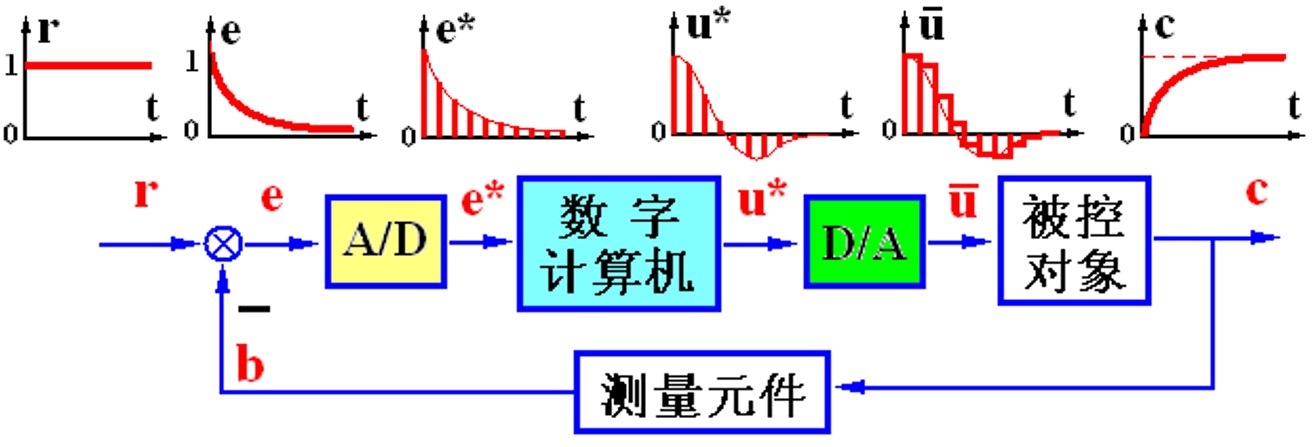
最主要的,数字系统和连续系统里面不一样的,是AD和DA转换还有计算机控制过程,被控对象还是个连续的物理设备,如何用数学描述这些不一样的地方呢?
在数学上可以认为A/D过程是个理想采样过程,即采样是理想采样(瞬间完成),量化误差(字长足够)也忽略不计了。
\[\tau << T, e^*(kT) = e(kT)\]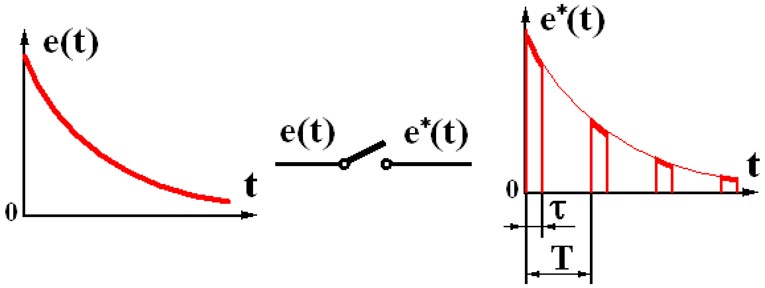
计算过程描述成数码量通过一个连续系统后再次采样。
比如实际系统,MCU输入为 signed int error,输出为signed int u,数学上MCU内部的算法计算仍为\(G_c(s)\),只不过后面又跟了个理想采样过程,相当合理。

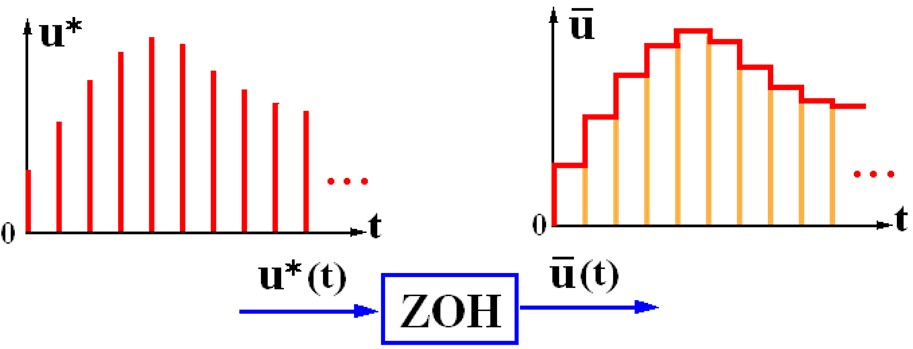
D/A过程在数学上用ZOH(零阶保持器)来描述,把离散数值保持一拍,使得连续时刻每刻都有个值,虽然不光滑但是连续了。
接着MCU输出了signed int u,后面跟一块DA芯片,就描述成这个样子。
现在常用的MCU比如,STM32或者NXP之类的,自带DAC模块了,这个过程实际上也是单片机里面内在的,比如说STM32,调用DAC_SetChannel1Data(DAC_Align_12b_R, vol);函数以后重新设置DAC的值,在此之前电压值就是上次设置的值。
实际上寄存器这个东西就是ZOH,只要不改变存储值,这个值一直即不会变。
将上面过程画成数学上的表达方式
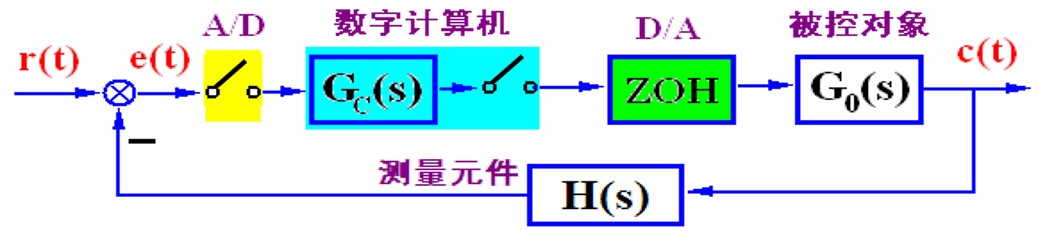
信号采样序列\(\delta_T(t) = \sum_{-\infty}^{+\infty} \delta(t - nT)\),调幅信号是载波乘信号生成的,离散信号类似,单位脉冲序列乘时间域信号就是一串离散信号。
信号采样的数学表达\(e^*(t) = e(t) \cdot \delta_T(t) = \sum_{0}^{+\infty} e(nT) \cdot \delta(t - nT)\)
这个误差采样的拉普拉斯变换
\[E^*(s) = \mathscr{L} \left[ e^*(t) \right] = \mathscr{L} \left[ \sum_{0}^{+\infty} e(nT) \cdot \delta(t - nT) \right] = \sum_{0}^{+\infty} e(nT) \cdot e^{-nTs}\]也就是说,e(nT) 延迟了nT出现了。即第n拍出来值为e(nT)这个值。
一个连续信号拉普拉斯变换是个s的有理式,离散化以后,拉普拉斯变换是个级数和,所以分析起来就不是很容易。
E*和E的区别有多大呢,将采样序列做傅里叶变换后带入进行拉普拉斯变换,可以知道关系 \(E^*(s) = \frac{1}{T}\sum_{-\infty}^{+\infty} E( s + jn\omega_s)\)
区别于前面给出E*与et在采样点上取值之间的关系,一般可以写成封闭形式。这个式子给出了E*与E之间的关系,用于e*的频谱分析。
频谱是对信号而言,频率特性是对系统而言,对于一个给定的信号e(t),非周期信号的频谱是连续的。采样后的离散信号的频谱可以用上面的关系,可以看出是连续频谱平移后叠加。
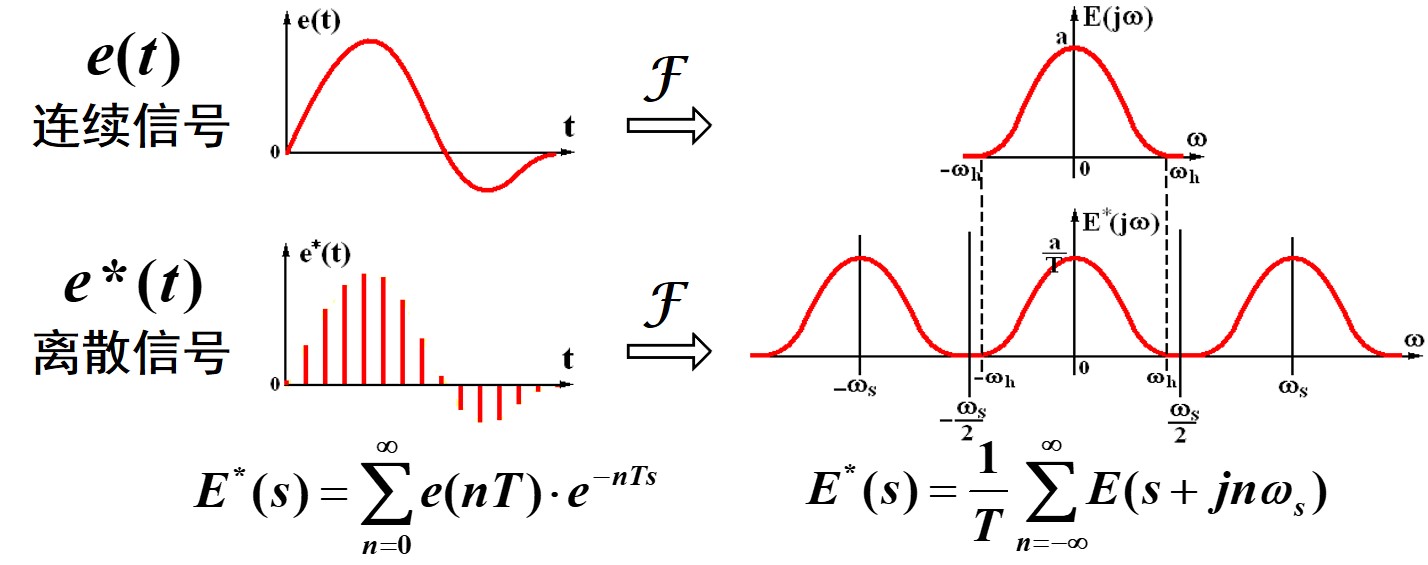
很重要的一个事情,采样频率必须足够快,才能不丢失连续信号的信息。这就是香农采样定理
\[\omega_s > 2\omega_h\]采样频率足够高后,找个理想滤波器,把高频的全部过滤掉,信号就可以一模一样的复现出来了,只不过幅值差了一点点。
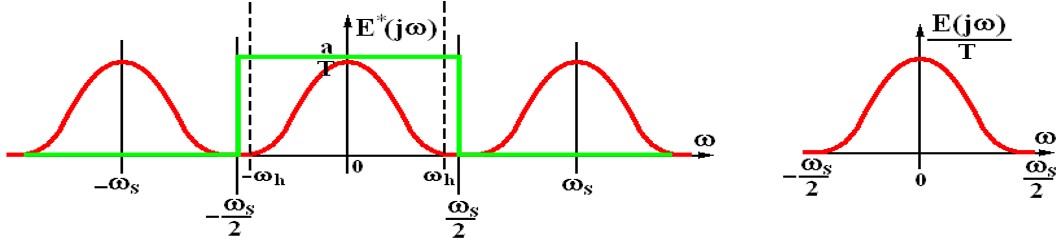
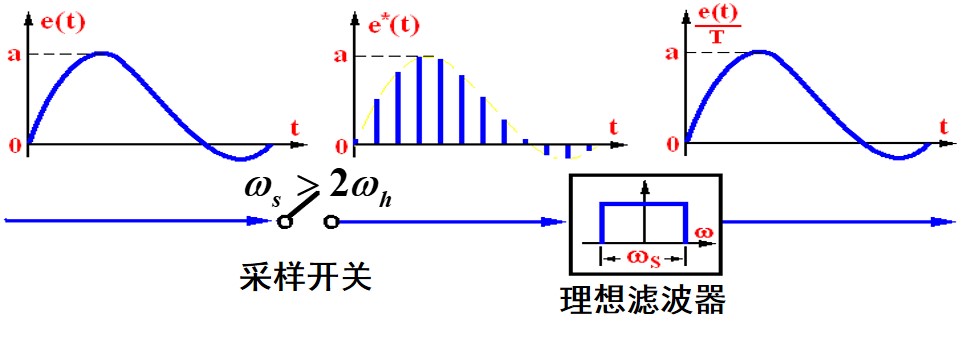
很遗憾理想滤波器物理上不可实现,但是有个差不多的,找个容易实现又接近的。零阶保持器。
时域表达
\[k(t) = 1(t) - 1(t-T)\] \[\color{red} { G_h(s) = \frac{1-e^{-Ts}}{s} }\] \[G_h(j\omega) = T\frac{\sin (\omega T/2)}{\omega T/2} e ^{-j\omega T/2}\]表达式略微复杂了一点,但是幅相特性还是可以画的
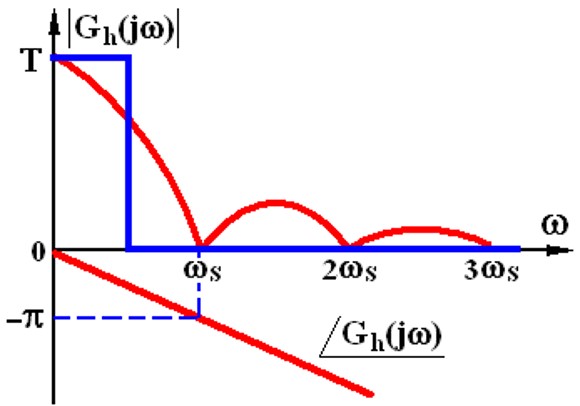
希望的理想滤波器的幅频特性是蓝线,相频特性是0,然而实际的ZOH的特性是红线,所以即便是满足了香浓采样定理,也是没法完全一模一样复现的。但是还是要精确的看看影响
ZOH把离散信号变成阶梯信号,粗略的看,认为是加了一个T/2的纯延时环节,相角滞后了,稳定裕度损失了。所以ZOH对系统是有不利影响的。但是这点不利换来了巨大的其他便利。
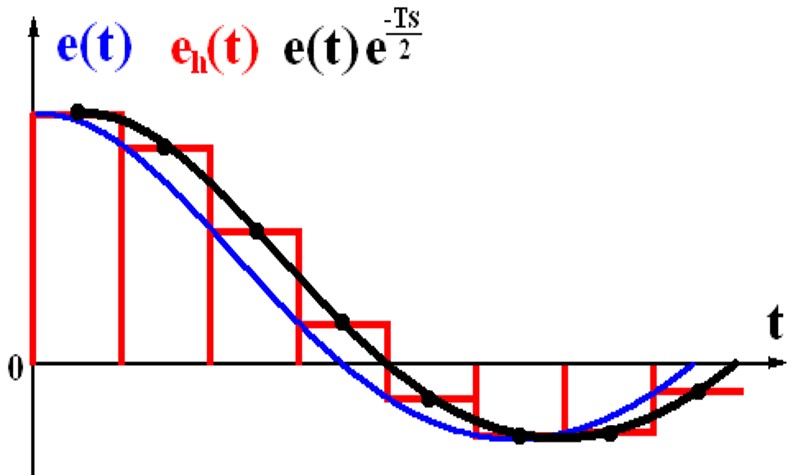
ZOH实际上不需要去实现,寄存器就是。而且可以严格证明,这个性能不算差,这个滞后效应比一阶二阶保持器都要小。
采样后送进MCU,运算输出后,复现的问题。
为什么可以离散的问题
离散域分析的数学工具
前面出现过,\(e^{Ts} = z\),可以认为就是个简单的代换。
究其本质,这是个复函数,这个代换实际上是个映射。复函数\(w = e^z\)代表的映射
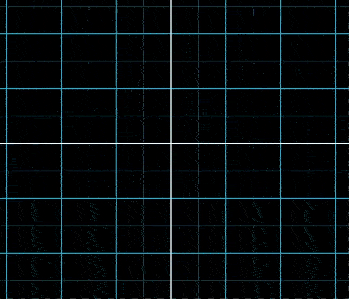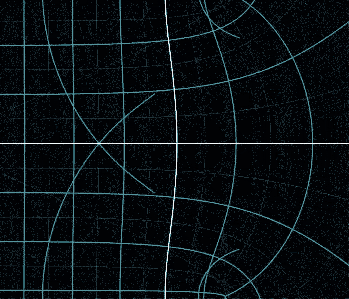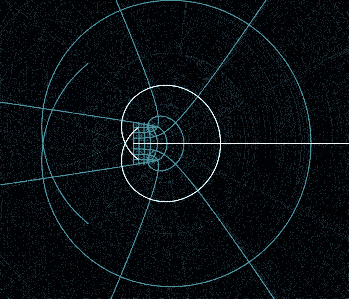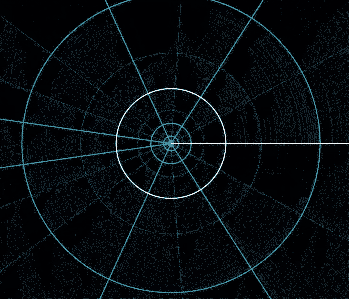
把这里个离散表达的东西放到一起
\[\begin{array}{} \left\{ \begin{align} e^*(t) &= \sum_{0}^{+\infty} e(nT) \cdot \delta(t - nT) \tag{1}\\ E^*(s) &= \sum_{n=0}^{+\infty} e(nT) \cdot e^{-nTs} \tag{2}\\ E(z) &= \sum_{n=0}^{+\infty} e(nT) \cdot z^{-n} \tag{3} \end{align} \right. \end{array}\]核心都是在表达幅值为e(nT)的这个脉冲延迟了n拍出现,这里的求和是把单个脉冲加成连续的序列,而不是一点上值相加。这三个意思是一样的。
Z变换仅仅对离散信号而言,但是写法有好多
\[E(z) = \mathscr{Z} [e^*(t)] = \mathscr{Z} [E^*(s)]= \mathscr{Z} [E(s)]\]z变换的数学方法:级数求和法、部分分式展开法、留数法。
级数求和根据上面式子(3),算一个无穷级数,这就是纯数学方法了,先导后积或者先积后导这些可能也要用的。
部分分式展开需要熟悉基本的几个变换
| \(E(s)\) | \(e(t)\) | \(E(z)\) |
|---|---|---|
| \(1\) | \(\delta(t)\) | \(1\) |
| \(\frac{1}{s}\) | \(1(t)\) | \(\frac{z}{z-1}\) |
| \(\frac{1}{s^2}\) | \(t\) | \(\frac{Tz}{(z-1)^2}\) |
| \(\frac{1}{s^3}\) | \(\frac{t^2}{2}\) | \(\frac{T^2z(z+1)}{(z-1)^3}\) |
| \(\frac{1}{s+a}\) | \(e^{-at}\) | \(\frac{z}{z-e^{-aT}}\) |
同样的和拉普拉斯变换一样,也有一些Z变换的性质。最常用的,线性性质,位移定理。
最重要的,初值定理终值定理,这在连续系统里都有对应的东西,对照的看,工具性质的东西。连续系统的思想,离散的工具,具体的细节放在后面稳定稳态误差做对照。
还有个卷积定理。遇到了再说。
Z反变换:幂级数法(长除法)、部分分式展开法、留数法。
长除法最无脑,部分分式展开要记得除z,留数法最通用。
数学工具,z变换只局限在采样点去研究系统,这也是不得已而为之,和最后的连续的输出相比还是有差距。
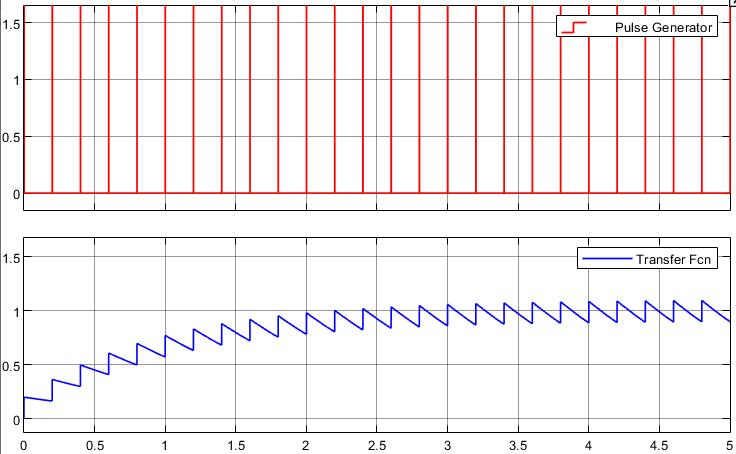
举个例子说明一下,用窄脉冲去模拟脉冲序列直接作用于一个连续系统
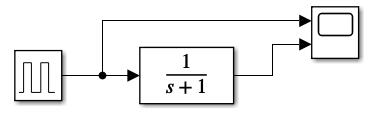
蓝线是实际响应曲线,但是虚设采样开关后只反映了采样时刻的信息。后面还会说虚设开关这个事情。
离散系统的数学模型
接下来要真正的找出离散系统的模型。
差分方程
离散系统的时域数学模型:差分方程。
差分有个前向后向的问题,前向是往未来操作(前进),后向是往过去操作(后退)。
前向差分:
\[\Delta e(k) = e(k+1) - e(k)\] \[\Delta^2 e(k) = \Delta e(k+1) - \Delta e(k)\]后向差分:
\[\nabla e(k) = e(k) - e(k-1)\] \[\nabla^2 e(k) = \nabla e(k) - \nabla e(k-1)\]对比连续的微分
\[\lim_{T \to 0} \frac{\Delta e(k)}{T} = \frac{de(t)}{dt}\]相应的,差分方程有前向差分、后向差分,解法有迭代法、Z变换。
对于离散系统,解出差分方程自然也就有时域解了,系统的特性也就知道了。
脉冲传递函数
差分方程对应微分方程,相应的脉冲传递函数对应传递函数。脉冲传递函数定义为零条件输出z变换比输入z变换。
对于一个系统,有时候需要虚设一个开关,放弃部分输出信息,退一步用离散的方法还可以进行分析。
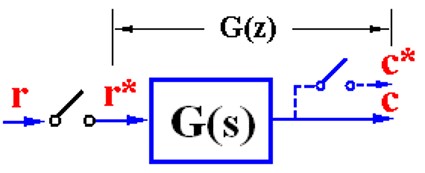
放弃一部分输出信息后使用z变换就可以得到离散数学模型,脉冲传递函数:
\[G(z) = \frac{C(z)}{R(z)}\]类比连续系统,也是单位脉冲响应的Z反变换。
同样的类比连续传递函数,这是个z的复函数,也由系统结构参数确定,等价于差分方程,同样可以画出z平面的零极点图。
当然脉冲传递函数也有局限性,无法反映系统响应的全部信息(仅采样点);只适用单入单出、线性定常。
开环脉冲传递函数
由实际系统各模块画出控制框图以后,同样面临着找出脉冲传递函数的问题,由于由采样开关的问题,和连续系统还稍稍有点不一样。
- 环节之间有采样开关
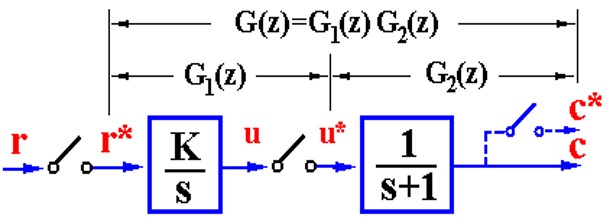
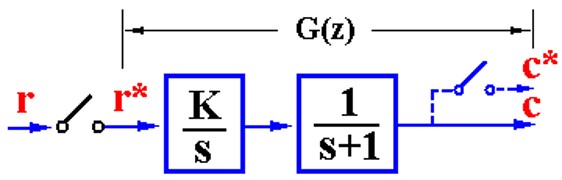
- 环节无开关的处理方法
- 有零阶保持器的处理
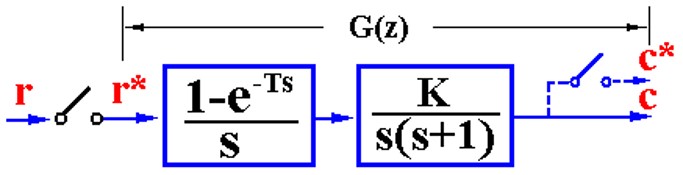
前面频率里推到过ZOH的传递函数,这里看看串联进去改怎么处理。把ZOH拆开来,可以看出虽然ZOH有积分环节但是并不增加系统阶数。
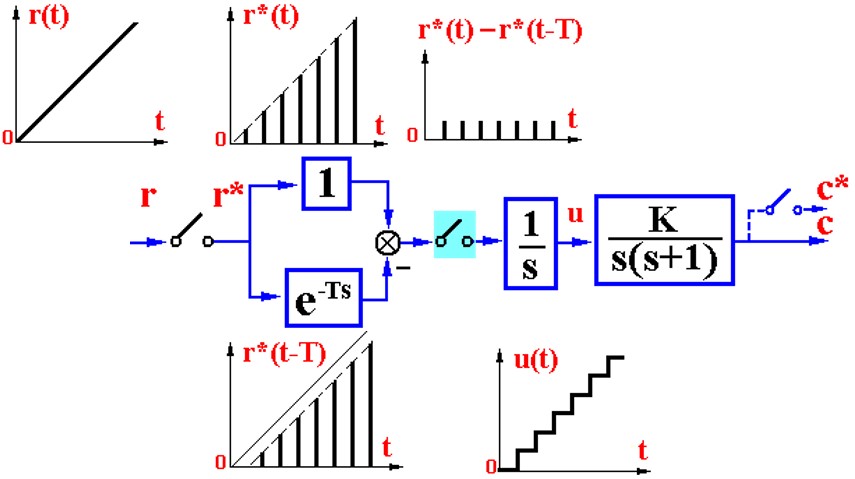
闭环脉冲传递函数
闭环系统脉冲传递函数,这是最后要用的东西。在这里Mason公式是有条件的。
再找闭环脉冲传递函数的时候,采样开关有时候需要等效,思想大概就是早晚都要采样,不如提前采样。
找闭环脉冲传递函数跟着信号流动方向硬推肯定是没问题的,虽然略微复杂。要注意前面一块Z变换还是分开Z变换的问题。
对于Mason公式,从数学方法的角度去考虑,改变字母并不会改变公式本质,所以每个环节前后都有采样开关或者等效采样开关的话,是可以直接用Mason公式的。
此外只有一个回路(无前馈通道),在前向通道至少存在一个一个实际采样开关的系统也可以小用一下。
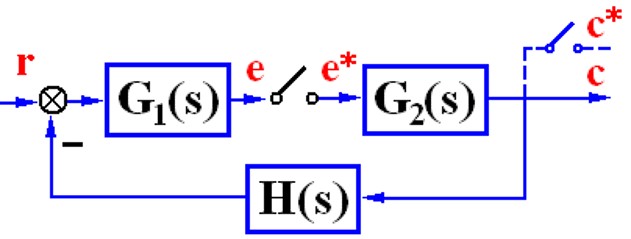
这种系统采样开关没法透过G1,输入是连续,这种情况一般求不出脉冲传递函数,只能求出输出的z变换C(z),但是只要输出的有了不影响分析,有个技巧,认为输入的r是单位脉冲激励的,开始的一瞬间给一下后面就没关系了。
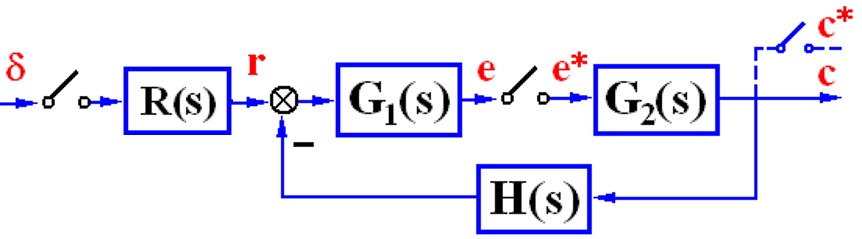
这样的话就有
\[\frac{C(z)}{1} = \frac{RG_1(z)G_2(z)}{1 + G_1G_2H(z)}\]信号的分解
卷积的本质是信号的分解
基本信号及响应,信号的分解,
连续信号分解成\(\delta(t)\)的线性组合,这样线性是不变系统就好搞了。
\[f(t) = \int_{-\infty}^{+\infty} f(\tau)\delta(t-\tau)d\tau\]这个积分是时间上加成一个序列,并非一个点上的数值相加。放在离散系统可能更好理解。
相当于把一个连续信号看作是一堆脉冲输入到系统里。
\(\delta(t-\tau)\)的输出为\(h(t-\tau)\)
那么总的输入\(f(t) = \int_{-\infty}^{+\infty} f(\tau)\delta(t-\tau)d\tau\)的输出为
\[y(t) = \int_{-\infty}^{+\infty} f(\tau)h(t-\tau)d\tau\]这个式子叫成卷积积分,直接在时域里面得到了响应。
更数学的定义:
\[f(t) = f_1(t)*f_2(t) = \int_{-\infty}^{+\infty} f_1(\tau)f_2(t-\tau)d\tau\]卷积完还是个函数。纯时域的操作。
在复频域来看\(Y(s) = G(s)R(S)\)
取样序列
\[\delta(k) = \begin{array}{} \left\{ \begin{align} = 1 , \ \ \ k=0\\ = 0 , \ \ \ k \ne 0\\ \end{align} \right. \end{array}\] \[\delta_T(t) = \sum_{n=0}^\infty \delta(t-nT)\]同样这个一串序列也是时间上把一个个脉冲加起来,不是说一个点把值加起来。
信号与系统里面有序列的分解。
任意离散序列\(f(k) = \sum_{-\infty}^{+\infty} f(i)\delta(k - i)\)
