概率基础
概率的直观想法
古典概型属于是概率入门了,就是很容易进行直观理解的概率,典型的袋子里面拿球。但是呢,这个东西在大学数学里并不是重点,甚至一笔带过了,不是概率论里核心的主线的东西。
几何概型有点数学工具的东西在里面了。
真正使用函数工具表示概率才是主线内容,借助强大的微积分工具,可以从各个角度下手。
我个人认为概率是一个比较难思考的科目,定理公式的含义比线性代数还要难思考,一件挺复杂的事情用几个符号就代表出来了,高度精简,但是一个式子后面其实讲了很多事情。
我本科概率论和统计考试考了89分,然而过了两个星期全忘了,这全要得益于高度抽象,因为考试我像背单词一样背公式,应付一些概率计算和推理题是没有任何问题的。所以隔段时间就全忘了。再拿起来来看看又会做题了,过段时间又忘了。
事情之间的关系
这一块属于基础。对事件的抽象和描述,以及事情之间的关系。
- 包含
A包含于B,B包含A,一个意思。需要注意的是,A发生必然导致B发生。
- 互斥
AB无相同样本点,则互斥。
\[P(AB) = 0\] \[P(AB) = P(A) + P(B)\]互斥,互不相容。
- 对立
\(P(AB)=0\),而且\(P(AB)=P(A)+P(B)=1\)。
性别一种对立事件。一个人,从生物学上讲不是男就是女,不可能即男又女,且必为男或女。
类似的例子:抛硬币。
\(A\) 与 \(\bar A\)对立。
- 独立
基本概率公式
此外有个全新的东西条件概率,以及衍生出来的贝叶斯乱七八糟
样本点\(\omega\),样本空间\(\omega, \omega \in \Omega\),随机事件是样本空间的子集、即事件A、B、C等。
事件的基本关系有包含、相等、互斥(或互不相容 \(AB = \emptyset\) )、对立(\(A和\bar{A}\))。
事件的独立性P(AB)=P(A)P(B),区别互斥。
要着重理解三个描述事件的概念:对立、互斥(互不相容)、独立。
互斥事件:我有个宠物,既是猫又是狗,不可能发生,互斥事件。
AB不能同时发生,那么就是互斥事件有\(P(AB)=0, P(AB)=P(A)+P(B)\)
AB能同时发生,非互斥事件。如果\(P(AB)=P(A)P(B)\)那么独立,否则\(P(AB)=P(A)P(B \mid A)\)
独立事件:我周末吃烧烤的概率是20%,喝可乐的概率是90%,一边吃烧烤一边和可乐的概率是5%,吃烧烤和喝可乐是互不影响的独立事件吗?0.2*0.9=0.18≠0.05。可能我吃烧烤的时候会喝啤酒,这两个事情互相有影响。如果我一边吃烧烤一边喝可乐的概率是0.18那么这两个就是独立事件,喝可乐不影响吃烧烤,吃烧烤不影响喝可乐。
AB是否可以同时发生? 是:非互斥事件。
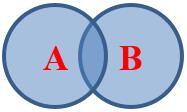
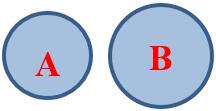
古典概型不学数学也会遇到这类问题。
几何概型属于升级一点的
