矩阵分解与广义逆

本章主要介绍矩阵的一些常用分解方法和 Moore-Penrose 广义逆矩阵的概念、性质、计算方法及其应用。

§1 三角分解、矩阵的满秩分解，矩阵的奇异值分解# §2 Penrose 方程， {1}-逆的计算及性质 §3 Moore.Penrose逆的计算及性质*

矩阵分解是将矩阵分解为两个或三个在形式上、性质上比较简单的矩阵的乘积。矩阵分解是求解线性方程组、处理各类最小二乘问题和最优化问题的主要工具。

LU 分解
Doolittle 分解
选列主元的 Doolittle 分解
Cholesky 分解

LU 分解

一个矩阵如果可以分解为上三角矩阵和下三角矩阵乘积的形式，就称可以进行三角分解。

进一步的，LU 分解 (lower–upper decomposition, LU decomposition)或者叫做 Doolittle 分解：

一个方阵 \(\boldsymbol{A} \in \mathbb{C}^{n \times n}\)，分解为一个下三角矩阵(lower triangular matrix ) \(\boldsymbol{L} \in \mathbb{C}^{n \times n}\) 和上三角阵(upper triangular matrix) \(\boldsymbol{U} \in \mathbb{C}^{n \times n}\) 的乘积，即

\[\boldsymbol{A} = \boldsymbol{LU}\]

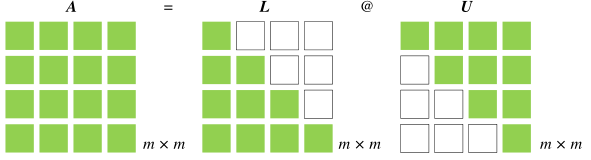
LU 分解的存在条件：\(\boldsymbol{A} \in \mathbb{C}^{n \times n}\) 的前 \((n - 1)\) 阶顺序主子式都不为 \(0\)。

具体的分解方法，可以写成 \(\boldsymbol{LU}\) 的形式，反推计算。

当这种情况有 \(u_{ii} = 0\) 或者值很小的时候，在计算机计算时会出现错误或者溢出，需要改进。这就是选列主元的 Doolittle 分解。

补充

主元，即起主导作用的元素。最大值

选主元是控制误差的一种方式。

函数 scipy.linalg.lu() 默认进行 PLU 分解

如果矩阵能够分解为三角矩阵的乘积，那么三角矩阵的特殊形状及良好的运算性质将对求解矩阵行列式、矩阵的逆及线性方程组等问题有很好的帮助。最基本的 LU 分解。更特殊的形式 Doolittle 分解，在 Doolittle 分解的过程中，如果矩阵 U 的主对角线元素为零或很小时，分解将出现中断或溢出，为了克服这个缺点，我们需要在分解过程中加入选列主元步骤，这就是选列主元的 Doolittle 分解。

Cholesky 分解

当矩阵 A 为 Hermite 正定矩阵时，A 可以分解为更特殊的形式，且无须选主元，这就是Cholesky 分解。

\[\boldsymbol{A} = \boldsymbol{LL}^T\]

进一步，可以有 LDL 分解，剪切-缩放-剪切

满秩分解

满秩分解是将非零矩阵分解为一个列满秩矩阵与一个行满秩矩阵乘积的形式，它是研究和计算矩阵广义逆等问题的有力工具，同时，在机器学习、模式识别、人工智能等方面也发挥着重要作用。

设 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}_r\)，如果存在 \(\boldsymbol{F} \in \mathbb{C}^{m \times n}_r\) 和 \(\boldsymbol{G} ^{r \times n}_r\) 使得 \(\boldsymbol{A} = \boldsymbol{FG}\) ，则称为 \(\boldsymbol{A}\) 的满秩分解。

满秩分解总是存在的但不唯一。

手算满秩分解：

一个矩阵进行初等变换，可以化为：

\[\boldsymbol{SAT} = \left [ \begin{array} {} \boldsymbol{I_r} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{array} \right ]\]

有

\[\boldsymbol{A} = \boldsymbol{S}^{-1} \left [ \begin{array} {} \boldsymbol{I_r} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{array} \right ] \boldsymbol{T}^{-1} = \boldsymbol{S}^{-1} \left [ \begin{array} {} \boldsymbol{I_r} \\ \boldsymbol{0} \end{array} \right ] \left [ \begin{array} {} \boldsymbol{I_r} & \boldsymbol{0} \end{array} \right ] \boldsymbol{T}^{-1} = \boldsymbol{FG}\]

仅使用初等行变换得到的 0 最多的形式称为 Hermite 标准形，即 \(\boldsymbol{SA} = \boldsymbol{H}\)

则找 \(\boldsymbol{S}\) 的方法 \([\boldsymbol{A},\boldsymbol{I}_m] \to [\boldsymbol{H}, \boldsymbol{S}]\)

找 \(\boldsymbol{T}\) 就很容易了

\[\left [ \begin{array}{} \boldsymbol{H} \\ \boldsymbol{I_n} \end{array} \right ] \to \left [ \begin{array}{} \left [ \begin{array}{} \boldsymbol{I_r} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{array} \right ] \\ \boldsymbol{T} \end{array} \right ]\]

这个方法比较复杂，还有更简单的方法，处理为 Hermite 标准形后。取 \(\boldsymbol{A}\) 的列拼成 \(\boldsymbol{F}\) 和 \(\boldsymbol{H}\) 的行拼成 \(\boldsymbol{G}\)

SVD 分解

奇异值分解是矩阵分析中一种重要的矩阵分解，是实对称矩阵对角化的推广。在信号处理、图像压缩、最小二乘问题、广义逆矩阵及统计学等方面都有重要的应用。

特征值，取定一组基，AD转换器，变换前后同一组基，最简单的表示，揭示映射最本质的。对角阵，意思是，基向量在引射下，只是把基向量承了个系数，即特征值。特征值是这么来的。

但是最早，不是去找最简单的映射这么来的。最早，就是用来解方程的，早些年，就是在找一个矩阵的数值特征。

对于 \(A\) ，为何会去讨论 \(AA^H\) 或者 \(A^HA\)呢？以前讨论过最小二乘解的问题，同解，等价的，\(Ax = b\)，一般矩阵性质不好，弄成性质更好的， \(AA^H\) 是半正定 Hermite 矩阵。可以酉对角化。

\(AA^H\) 的特征值，就是原矩阵的奇异值的开方。

奇异值分解是常用的。最早是用在条件数的，条件数描述矩阵性态，病态，。

一个矩阵的好坏，用条件数衡量。条件数大，是病态的。

解方程，用欧氏空间的旋转来消元，这种情况下会保持误差，不会让误差变得更大。

手算不要紧，但是电脑计算，float可表示的数总共只有 \(2^{32}\) 个，连有理数集合都填不满。

最大特征值开方就是最大正奇异值。二范数的话，条件数就是最大奇异值/最小奇异值。

特征值摄动。

F范数，

广义逆矩阵

广义逆矩阵的提出源于线性方程组的求解，它是数理统计、最优化理论、现代控制理论、网络系统、数字图像处理等科学的重要理论基础，并已成为实际工程中广泛使用的重要计算工具。

背景

考虑一个线性方程组的求解问题

\[\boldsymbol{Ax} = \boldsymbol{b} \tag{1}\]

其中 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}\)， \(\boldsymbol{x} \in \mathbb{C}^n\)， \(\boldsymbol{b} \in \mathbb{C}^m\)

当 \(m = n\) ，且 \(\boldsymbol{A}\) 可逆时，方程组 \((1)\) 有唯一解

\[\boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b} \tag{2}\]

然而，在很多实际问题中方程组 \((1)\) 的系数矩阵 \(\mathbb{A}\) 不可逆，或者甚至根本就不是方阵，但是方程组的解却是存在的。我们还想用类似于 \((2)\) 的简洁形式来表示方程组的解。因此就需要对通常意义下的"逆矩阵"概念进行推广，这就是广义逆矩阵。

概念

设 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}\)，一个矩阵 \(\boldsymbol{X} \in \mathbb{C}^{m \times n}\) 如果满足下列条件的其中几个

(1) \(\boldsymbol{AXA} = \boldsymbol{A}\)
(2) \(\boldsymbol{XAX} = \boldsymbol{X}\)
(3) \(\boldsymbol{AX}^H = \boldsymbol{AX}\)
(4) \(\boldsymbol{XA}^H = \boldsymbol{XA}\) 则称 \(\boldsymbol{X}\) 为 \(\boldsymbol{A}\) 的广义逆矩阵。

这 4 个方程为 Penrose方程。满足全部方程的广义逆矩阵称为 \(\boldsymbol{A}\) 的 Moore-Penrose 逆，记作 \(\boldsymbol{A}^+\)。

Moore-Penrose逆计算

1.广义逆矩阵的直接计算方法广义逆矩阵是通常逆矩阵的推广，这种推广的必要性，是线性方程组的求解问题的实际需要。在实际问题中，线性方程组的系数矩阵并不都是方阵，即使是方阵也不都是非奇异的，因此，有必要推广矩阵逆的概念。目前，关于Moore-Penrose逆的计算方法很多，本节我们介绍利用矩阵的奇异值分解和满秩分解的直接计算方法。

奇异值分解计算 \(\boldsymbol{A}^+\)

矩阵 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}_r\) 的奇异值分解为

\[\boldsymbol{A} = \boldsymbol{U} \left [ \begin{array} {} \Sigma & 0 \\ 0 & 0 \end{array} \right ] _{m \times n} \boldsymbol{V}^H\]

则

\[\boldsymbol{A}^+ = \boldsymbol{V} \left [ \begin{array} {} \Sigma^{-1} & 0 \\ 0 & 0 \end{array} \right ] _{m \times n} \boldsymbol{U}^H\]

满秩分解计算 \(\boldsymbol{A}^+\)

矩阵 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}_r\) 的满秩分解为 \(\boldsymbol{A} = \boldsymbol{FG}\) 则

\[\boldsymbol{A}^+ = \boldsymbol{G}^H (\boldsymbol{GG}^H)^{-1} (\boldsymbol{F}^H\boldsymbol{F})^{-1}\boldsymbol{F}^H\]

满秩分解这个式子是怎么来的？

对于广义逆矩阵一定有 \(\boldsymbol{AXA} = \boldsymbol{A}\) ，矩阵 \(\boldsymbol{A}\) 不一定是可逆的，但是可以想办法写成两个满秩矩阵的乘积即 \(\boldsymbol{A} = \boldsymbol{FG}\)，那么表达式可写为 \(\boldsymbol{AXA} = \boldsymbol{\color{red}{F} \color{black}GXF \color{red}{G}} \color{black}= \color{red}{\boldsymbol{FG}}\)

想让右边的成立，很自然的想法是里面的 \(\boldsymbol{GXF} = \boldsymbol{I}\) ，那这不就可以了。

然而分解出来的 \(\boldsymbol{F}\)，\(\boldsymbol{G}\) 虽然是满秩的，但不一定是方阵，没法谈可逆这个事情(广义逆正在解决)。为此又想到了 \(\boldsymbol{GG}^H\) 是方阵，并且，是满秩的，一定可逆，逆为 \((\boldsymbol{GG}^H)^{-1}\)，事实上到这里，表达式已经出来了。

迭代计算

在Moore-Penrose 逆的直接计算解法中，往往需要对矩阵 A 进行各种形式的分解，但实际计算中这种分解是比较困难的。因此，在实际计算中，常常用迭代法来计算 Moore-Penrose 逆的近似矩阵。本节将介绍计算 Moore-Penrose 逆的几种矩阵迭代方法和 Greville 递推法。

Moore-Penrose逆性质

矩阵的Moore-Penrose逆同时满足四个Penrose方程，它具有所有广义逆矩阵的所有性质，同时也具有一些特殊的性质。本节将介绍Moore-Penrose逆的一些基本性质和它在求解线性方程组中的应用。在这一节，我们将看到Moore-Penrose逆和方阵的逆在性质方面的重要区别及如何利用广义逆矩阵把线性方程组的通解、极小范数解概括和统一起来。

(1) \((\boldsymbol{A}^+)^+ = \boldsymbol{A}\)
(2) \((\boldsymbol{A}^+)^H = (\boldsymbol{A}^H)^+\)，\((\boldsymbol{A}^+)^T = (\boldsymbol{A}^T)^+\)
(3) \((\lambda\boldsymbol{A})^+ = \lambda^+ \boldsymbol{A}^+\)，\((\boldsymbol{A}^+)^T = (\boldsymbol{A}^T)^+\)

Moore-Penrose逆应用

线性方程组的问题

设 \(\boldsymbol{A} \in \mathbb{C}^{m \times n}\) ，\(\boldsymbol{b} \in \mathbb{C}^m\)，则 \(\boldsymbol{Ax} = \boldsymbol{b}\) 有解的充要条件是 \(\boldsymbol{AA}^+\boldsymbol{b} = \boldsymbol{b}\)，并且通解为

\[\boldsymbol{x} = \boldsymbol{A}^+\boldsymbol{b} + ( \boldsymbol{I} - \boldsymbol{A}^+\boldsymbol{A})\boldsymbol{x}_0 \tag{1}\]

其中 \(\boldsymbol{x}_0 \in \mathbb{C}^n\) 为任意向量。

如果解不唯一，那么唯一极小范数解为

\[\boldsymbol{x}_0 = \boldsymbol{A}^+ \boldsymbol{b} \tag{2}\]

【扩展】

如果 \(\boldsymbol{Ax} - \boldsymbol{b} \ne 0\) 永不成立，我们还想找出一个向量，使得距离给定向量最近。(空间的角度来理解，这里缺个图，最佳逼近问题，最优问题)。即 \(\Vert \boldsymbol{Ax} - \boldsymbol{b} \Vert_2\) 最小，这个解就是最小二乘解。

最小二乘解

\[\boldsymbol{x} = \boldsymbol{A}^+\boldsymbol{b} + ( \boldsymbol{I} - \boldsymbol{A}^+\boldsymbol{A})\boldsymbol{x}_0 \tag{3}\]

极小范数最小二乘解

\[\boldsymbol{x}_0 = \boldsymbol{A}^+ \boldsymbol{b} \tag{4}\]

可以看出，概念的推广让方程组解的含义更丰富了。