系统的的复频域分析

The Root Locus Method

实际上传递函数就是个复变函数， $s$ 是个复变量，传递函数是在复域讲的。这里的复频域分析指的是根轨迹，意思是在 $s$ 平面上研究系统的性能。具体研究的范围：某一参数变化对闭环系统极点（系统性能）的影响。

这是个很重要的图解法，某一参数的变化对闭环极点位置的影响。闭环极点位置随着参数变化而运动的轨迹就是根轨迹。这个根指的是闭环传递函数分母为0的根，即特征方程的根，也就是闭环极点。所以根轨迹能直接看出系统的稳定性如何，性能大概是啥样，实质是 $D (s) = 1 + G (s) H (s) = 0$ 的解。

这个方法再早些年还没计算机的时候应该时挺好用的，比如说做比例控制的时候，确定一个差不多的增益，直接跟着感觉画画，闭环极点的运动轨迹就有了，系统稳定性也可以看个大概了。如果有人说你这也不精确啊，工程嘛，大差不差，还有一部分东西是试出来的。

根轨迹是个什么含义？

根轨迹的含义：开环传递函数参数变化时，闭环特征方程的根在 $s$ 平面上的运动轨迹。根轨迹图上的零极点是开环传递函数的，但是轨迹上的点都是闭环特征方程的极点。

提示

The root locus is the path of the roots of the characteristic equation traced out in the 𝑠-plane as a system parameter is changed.

一个系统为：

开环传递函数为 $G (s) H (s)$ ，根轨迹增益写零极点形式即首1型：

G (s) H (s) = \frac{K^{*} \prod_{i = 1}^{m} (s - z_{i})}{\prod_{j = 1}^{n} (s - p_{j})}

闭环传递函数为：

Φ (s) = \frac{G (s)}{1 + G (s) H (s)}

闭环特征方程的解即极点决定了系统的稳定性，闭环极点满足下面这个式子：

1 + G (s) H (s) = 0

也就是

\begin{matrix} (*) & G (s) H (s) = - 1 \end{matrix}

闭环系统的极点满足*式， $G (s) H (s)$ 东西还正好是开环传递函数，就是这么巧。再进一步，*式叫根轨迹方程，作为一个复数表达式，换个形式可以写成有幅值相角，也就是极点轨迹的幅值条件(Magnitude criterion)和相角条件(Angle criterion)：

| G (s) H (s) | = K^{*} \frac{\prod_{i = 1}^{m} | (s - z_{i}) |}{\prod_{j = 1}^{n} | (s - p_{j}) |}

∠ G (s) H (s) = \sum_{i = 1}^{m} ∠ (s - z_{i}) - \sum_{j = 1}^{n} (s - p_{j}) = (2 k + 1) π

相角条件是点在根轨迹上的充要条件；该点对应的 $K *$ 值，由幅值条件求出。

考试比较看重的根轨迹画法实际上全是两个条件推出来的二级结论。

广义根轨迹

我觉得人的思维比较强的地方就是演绎，比如货币可以不足值，演绎一下就有了0价值的纸币，挺有意思。广义根轨迹就是根轨迹的一个演绎，通过一些奇思妙想，充分的在不同地方使用同一个工具。有了负反馈条件下的根轨迹，有时候需要用到正反馈条件下的根轨迹，还有除了根轨迹增益之外其他参数变化时的根轨迹，通过一个巧妙的转化，实际上还是普通根轨迹的那些东西。

参数根轨迹

这里还是举例子吧，比如说对于一个单位反馈系统的开环传递函数：

G (s) = \frac{(s + a) / 4}{s^{2} (s + 1)}

这个问题，如果把 $a$ 提出啦，表面是个根轨迹增益形式，但是这么处理零点也在跑，所以不能这么处理。但是对于这个开环传递函数，系统的闭环传递函数分母（特征多项式）是 $D (s) = s^{3} + s^{2} + s / 4 + a / 4 = 0$ ，有个好玩的事情，这个特征多项式也适用于这个开环传递函数：

G^{*} (s) = \frac{a / 4}{s (s + 1 / 2)^{2}}

这个等效传递函数的根轨迹我是会画的，因为根轨迹指的是闭环传递函数特征多项式的极点运动轨迹，所以两个传递函数画出来的是一个根轨迹。但是画完以后，就不用这个等效的了，还是用原来的来分析系统性能。

零度根轨迹

系统实际为正反馈时候的根轨迹。

根轨迹分析系统性能

本质上还是极点对系统的影响，不过不是固定极点了，因此要求特别熟悉极点零点位置与响应的关系。

根轨迹画法（8条法则）

这个怎么说呢，现在画根轨迹可以用matlab一个函数就完事了。所以我觉得对于理解来讲，这一部分并不是最重要的，因此这块内容被放到了最后面。

用matlab画根轨迹，举个例子，对于一个单位反馈系统开环传递函数为：

G (s) = \frac{K^{*}}{s (s + 1) (s + 2)}

num = [1];                             %开环分子多项式系数
den = conv([1,0],conv([1,1],[1,2]));   %开环分母多项式系数
sys = tf(num,den);                         
rlocus(sys);                           %画根轨迹
axis([-3 1 -3 3]);                     %坐标范围

运行一下

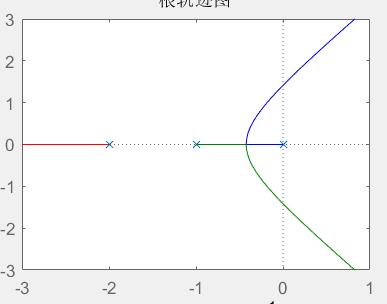
但是作为考试的话，还是个熟能生巧的事情，还得练练。就多画画，法则有8条：

1.起点终点

起于开环极点，终止于开环零点或无穷远。

（模值条件推）

2.分支数、对称性、连续性

根轨迹分支数=开环极点书=特征方程阶数；根轨迹上下对称且连续。

3.实轴上的根轨迹

最右侧开始数，奇数点到偶数点之间的是根轨迹。

（相角条件推）

重要

零度根轨迹：和这个刚好相反

4.闭环特征根之和为常数

当 $n - m \geq 2$ 时， $\sum_{i = 1}^{n} λ_{i} = C$

其实这个东西在二元一次方程里有个根与系数的关系。那么不负责任的猜想这个是不是在复数方程、高阶一元多次方程的推广呢？

这个定理的用处是有根往右跑，那么一定要有根往左跑。

5.渐近线

\begin{array}{l} {\begin{aligned} σ_{a} & = \frac{\sum_{i = 1}^{n} p_{i} - \sum_{j = 1}^{m} z_{j}}{n - m} \\ φ_{a} & = \frac{(2 k + 1) π}{n - m} \end{aligned} \end{array}

渐近线交点和渐近线夹角。

重要

零度根轨迹：

φ_{a} = \frac{2 k π}{n - m}

6.根轨迹分离点

\sum_{i = 1}^{n} \frac{1}{d - p_{i}} = \sum_{j = 1}^{m} \frac{1}{d - z_{j}}

7.与虚轴交点

临界稳定点。

$s = j ω$ 带入特征方程，有 $D (j ω) = 0$

8.出射角/入射角

\sum_{j = 1}^{m} ∠ (s - z_{j}) - \sum_{i = 1}^{n} ∠ (s - p_{i}) = (2 k + 1) π

重要

零度根轨迹：

\sum_{j = 1}^{m} ∠ (s - z_{j}) - \sum_{i = 1}^{n} ∠ (s - p_{i}) = 2 k + π

举例子

根轨迹更多的时感觉。零极点画出来，跟着感觉勾一下。所以还是得多看看怎么画，然后就有感觉了。