系统的频域分析

国外的一个可以交互的学习频域网站Linear Physical Systems Analysis-Bode Plots，有些例子还是很生动直观的。

频域分析是基于频率特性的图解法。首先得有频率特性的概念，用频率特性分析系统的稳定性是独立于前面方法。如果从电学系统的角度来看，前面是直流后面是交流，这是个很粗略的表述。频率特性没有前面的时域指标直观，在实际系统比如悬挂超调量是看的到的，然而裕度这个东西没法直接看到。

教材里大量的章节在讲画图方法，图解法的前提是先得有图，这个图还不是那么好画，如何画波特图和幅相图是一大块内容，而且还挺枯燥，画图这块内容并没有那种豁然开朗感觉很妙的控制理论的巧妙思想在里面，就是单纯的数学作图。需要多练习领会。

前面画的都是开环传递函数的图。控制系统稳定性的分析一直致力于通过开环判断闭环的稳定性。到了这里，奈奎斯特判据也是如此，特征方程仍旧是联系开环和闭环稳定性的关键。福相图里通过巧妙的映射，用开环幅相曲线和 \((-1,j0)\) 的位置关系来判断稳不稳。频域判据有个优势是判据除了判断稳不稳这个一刀切的指标，还能看出稳定程度，即相角裕度和幅值裕度。这是两个描述离不稳定界限还有多远的物理量，也是系统性能的频域指标，虽然从系统响应不能直接看出来，裕度和响应也是有联系的，可以通过频域指标去换算出时域指标。

从频域指标出发有三频段理论，这是使用频域校正的指导方向，后面校正再说。

最后还有一些闭环系统的指标，比如谐振、带宽等，在电子或通信系统里面常用到。

频率特性是什么

自动控制原理到了频域里感觉和信号与系统在一些思想上相通了。频率特性在控制理论的地位是相当重要的。具体有多重要呢？我也不知道， 。 总之感觉比时域根轨迹还重要。实际项目里见过画波特的图，但是不多见画根轨迹的。尤其是在模拟电路和电源设计里，基于频域分析的控制上的设计到处都是。

画图基本功

频域的图最重要的两个：幅相图、波特图。这两个里波特图又更常用，在模拟电路设计里面，波特图很多。

画波特图，对于最小相位系统来说，一般只画开环对数幅频特性，不画开环对数相频特性。但是要有看出相频特性曲线的能力。对数相频特性也是由典型环节叠加起来的，所以还是比较好考虑的。斜率决定相频的归宿，拉的越开，越接近这个斜率对应的典型特性的频率（我自己理解，可能没说明白。。。。而且这话也有漏洞）。斜率决定相角的极限，拉开范围决定了总幅值的影响程度。

频域下稳定性问题

Nyquist稳定判据

时域里有劳斯判据不解方程通过系数判断闭环系统稳定性。在频域里有奈奎斯特稳定性判据。

A frequency domain stability criterion called Nyquist stability criterion was developed by H. Nyquist in 1932.

对控制系统来说，稳定性问题是个基本问题，不仅仅是经典控制理论，现代控制、智能控制也是。稳定的充要条件，极点都在负半平面，Routh判据不解方程用系数判定，不但可以判定稳不稳，还可以知道负半平面有几个根。但是判据无法用来研究如何调整系统来改善稳定性。频域稳定性判据可以，也就是说Nyquist稳定判据既是判据，又能反映性能。

Nyquist稳定性判据也是不直接解根，而是用开环幅相特性直接判定闭环系统的稳定性。此外这个判据可以研究含有纯延时环节的系统，Routh判据做不到的。最重要的，这个判据可以给出系统结构的调整的方向，很猛，用起来很方便，所以这个东西在实际的控制工程里用的很广泛。

奈奎斯特稳定性判据的表达：

\[\color{red} {Z = P - 2N}\]

• Z：闭环不稳定极点个数
• P：开环不稳定极点个数
• N：开环幅相曲线包围\((-1,j0)\)点的圈数

这个 \(N\) 有正负号。人站在\((-1,j0)\)点，面对幅相曲线，逆时针包围是正。这和格林公式判断正负号一样，在操场上左手是足球场，那么说明跑步方向是对的。

说一下为啥是这样的，对于一个系统：

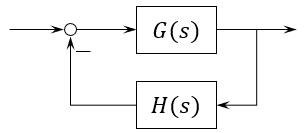
开环传递函数与闭环传递函数表达式：

\[G(s)H(s) = \frac{K^*M(s)}{N(s)}\] \[\Phi(s) = \frac{G(s)}{1+ G(s)H(s)} = \frac{N(s)G(s)}{N(s) + K^*M(s)}\]

这个 \(\frac{N(s)G(s)}{N(s) + K^*M(s)}\)是又往前算了一步，就是经常念叨的特征方程等于开环分子+分母，系统的稳定性关键在于\(D(s) = 1+ G(s)H(s) = 0\)。对于复函数：

\[F(s) = 1 + G(s)H(s) = 1 + \frac{K^*M(s)}{N(s)} = \frac{N(s) + K^*M(s)}{N(s)}\]

上面就是开环分子+分母，特征多项式，就是闭环极点；下面是开环极点。这个函数把开环极点和闭环极点联系了起来，并且分子分母阶数相同。要画\(F(s)\)的频率特性可以画\(G(s)H(s)\)的频率特性，然后搬一个单位，因为实部加个1，这时候这个-1已经察觉出来一点东西了。

这里面 \(F(s)\) 的稳定性是很好研究的，如果 \(F(s)\) 在右半平有Z个零点，P个极点，即Z个闭环极点，P个开环极点。在 \(s\) 平面，走一个奈奎斯特路径即一个封闭曲线，把右半平面的零极点包围起来，研究这过程中F的幅相特性曲线该怎么画。

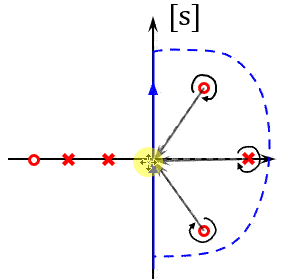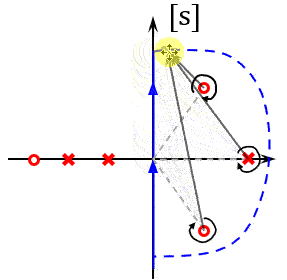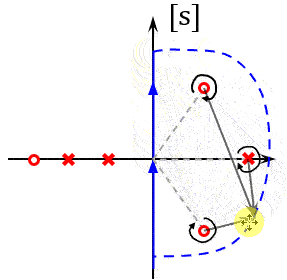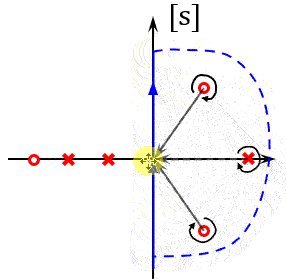
左半平面的点对角度没有贡献，但是右半平面的点对 \(F(s)\) 贡献的角度是一整圈角度为 \(2\pi\) 。F包围原点的圈数：

\[\angle F(j\omega) = -2\pi(Z-P) = 2\pi(P-Z) = 2\pi R\]

圈数是R，如果我知道F绕原点的圈数R，知道F的不稳定极点数P（开环不稳定极点数），那岂不是可以直接算出F的不稳定零点数Z（闭环不稳定极点数）。即\(Z = P - R\)，然而现在的问题是，\(F(j\omega)\)要是能画出来了，这都有Z和P了。

妙就妙在F的频率特性就是GH的频率特性向右搬动一个单位。当然这里还有个小问题，GH的频率特性是\(\omega :0\to + \infty\)，如果补全的画是\(-\infty \to + \infty\) 很容易看出是个对称关系，搬动一下，就是整个F的频率特性了。

那么就直接不要F包围原点了，只看GH包围\((-1,j0)\)了，最后的最后，GH是单边的，GH包围的圈数N是F包围圈数R的一半，2N = R。

对数稳定判据

搬移到波特图上。对数稳定判据是真正经典控制理论在电子学里面可以大有作为的地方。

\[\begin{array}{} \left\{ \begin{align} Z &= P - 2N \\ N &= N_+ - N_- \\ \end{align} \right. \end{array}\]

在bode图上，主要是看幅相图和bode的关系。幅相曲线和-1j0的关系，即单位圆外穿过负实轴的关系。在bode图上就是0db线上的部分，相频特性与-180°的关系。正负穿越指的是穿越-180°。这个事情在幅相图里也可以看，穿越负实轴的次数，这两个图是等价的。

由稳定性判据，两个衡量频域稳定程度的指标：相角裕度\(\gamma\)，幅值裕度\(h\)。

频域下的性能指标

系统动态性能和稳定程度，稳不稳是一刀切的指标，要么稳定要么不稳。动态性能和稳定程度相关，太稳了其实也不好，相应太慢太平缓，稳定的太不好也不好，晃荡半天停不下来。稳定程度要恰到好处，才能既平稳又快速。

稳定边界、稳定程度。时域法里面，稳定边界是虚轴，稳定程度是靠极点离虚轴远近衡量的，具体的数字量，借用二阶欠阻尼的阻尼比来描述。阻尼比太小，是稳定的，但是波动大；阻尼比过大，超稳定。频域里，稳定的边界，-1j0，如果研究的是最小相角系统（P=0），幅相曲线不包围就稳定，越过去就不稳了。那么稳定程度，就用距离来衡量。

稳定裕度

（稳定裕度）

频域里的两个指标，既能衡量稳定程度，又能看出系统性能，所以这个指标好啊。裕度有赋值裕度(Gain margin)和相位裕度(phase margin)

知道了稳定裕度，那么如何用开环频率特性分析系统的性能呢？

三频段理论

很重要的，三频段理论。开环对数幅频特性分成三个部分，一般的实际的一个开环系统的对数幅频特性曲线是左高右低的。认为截止频率附近为中频段；特别强调第一个转折频率左侧，基准线是低频段；低于0db线认为是高频段。

低频段与系统稳定精度相关：低频段画的是\(G_0(s) = \frac{K}{s^\nu}\)，所以低频段正好完全体现出了型别（斜率）、开环增益。低频段就这么多。

中频段，截止频率附近，与动态性能有关，可以读出相角裕度。对于最小相角系统，从头到尾都是-20，那么相角-90，相角裕度90°；如果从头到尾-40，相角裕度是0，斜率再大就不稳了。所以一个系统如果性能好的话，是要求中频段以-20的斜率穿越0dB线，可以保证有比较大的相角裕度。

高频段，决定闭环系统抗高频干扰的能力。对于开环来讲，高频段压的很低，自然可以将高频率信号过滤掉，但是在高频段有：

\[\Phi(s) = \frac{G(s)}{1 + G(s)} \approx G(s)\]

基于上面的描述，就有了一个比较理想的幅频特性曲线的样子：低频段决定稳定误差，希望是-20或-40，高一点。中频段决定动态性能，希望-20穿越0db线，而且要拉开。高频段直接描述闭环系统抗高频能力，希望压低。

三频段理论告诉我们理想的系统大概是什么样，这也是后面改造系统的努力方向。

前置知识：最小相角系统，看到幅频特性曲线，能想到相频特性曲线是什么样子。

欠阻尼二阶系统指标换算

中频段是我们特别关注的，前面只是说中频段和动态性能有关系，但是这还不够，还得知道具体关系。用个二阶系统具体来看一下频域指标和时域指标，还是典型欠阻尼二阶系统：

\[G(s) = \frac{\omega_n^2}{s(s + 2\xi\omega_n)}\]

这个频率特性表达式有：

\[\begin{array}{} \left\{ \begin{align} \mid G(j\omega) \mid &= \frac{\omega_n^2}{\omega\sqrt{\omega^2 + 4\xi^2\omega_n^2 }}\\ \angle G(j\omega)&= \\ \end{align} \right. \end{array}\]

总之截止频率是可以精确算出来的：

\[\omega_c = \omega_n \sqrt{\sqrt{4\xi^4+1} - 2\xi^2}\]

\(\omega_c\)是\(\omega_n\)的增函数，\(\xi\)的减函数。

相角裕度也是可以精确算出来的，尽管略微复杂：

\[\gamma = \arctan \frac{2\xi}{\sqrt{\sqrt{4\xi^4+1} - 2\xi^2}}\]

相角裕度只和阻尼比有关，而且是增函数。此外，超调量也仅和阻尼比有关。那么也就是说：

\[\gamma \iff \xi \iff \sigma \%\]

这三个量知道了一个，就可以知道另外两个。

最后还有个调节时间\(t_s = \frac{3.5}{\xi \omega_n}\)

可以通过这种方式联系起来：

\[t_s\omega_c = \frac{7}{\tan \gamma}\]

实际用的时候，看看函数曲线找值就好了：

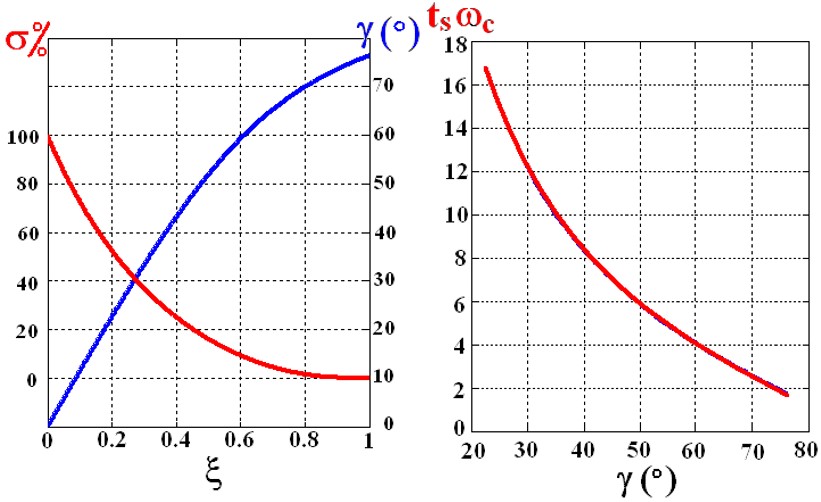
频域里面估计二阶系统性能指标没有优越性，但是，最重要的，我们是要在更高阶的系统里用这种估计方法。

高阶系统指标换算

从理论上分析很麻烦，但是控制前辈们经过大量工程实践，总结的公式，偏于保守，但是在\(35° \le \gamma \le 90°\)的常用范围内，精度是完全满足分析和设计的要求的

\[\begin{array}{} \left\{ \begin{align} \sigma\% &= \left[ 0.16 + 0.4 \left( \frac{1}{\sin \gamma} - 1 \right) \right] \times 100\% \\ t_s &= \frac{\pi}{\omega_c}\left[ 2 + 1.5 \left( \frac{1}{\sin \gamma} - 1 \right) + 2.5\left( \frac{1}{\sin \gamma} - 1 \right)^2 \right] \end{align} \right. \end{array}\]

先画对数幅频曲线，很容易算出截止频率，算相角裕度也很容易，多按几个arctan就行。

实际用的时候看看这个函数曲线就行了：

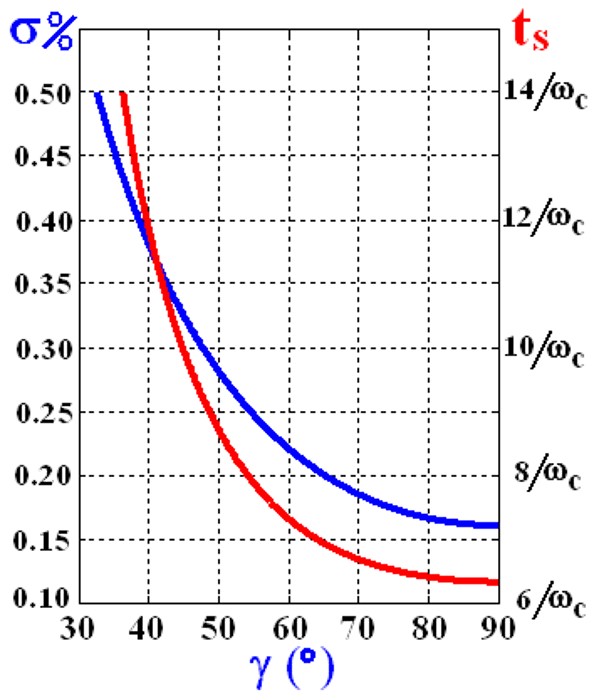
阶数越高，越好用。

闭环频率特性

前面是在讲通过开环分析闭环，现在是直接研究闭环的东西。

闭环的一些特征量在工程上用的很多比如带宽和带宽频率。此外闭环频率特性很容易测量，所以也有必要看看闭环频率如何估计系统性能指标。

实验测是一个方法，此外也可以用开环频率特性去得到闭环频率特性，（矢量法，方法跳过，没电脑这么做）。

闭环频率特性的几个特征参量：

• 零频值：\(M_0 = M(0)\)，实际上就是闭环增益。

• 谐振频率(the resonant frequency)、谐振峰值(The maximum value of the magnitude)，\(\omega_r, M_r\)

这个在典型二阶环节的时候说过，当时是站在闭环整体的角度说的。大闭环里的小闭环。但是要注意这实际上是频域指标。

典型欠阻尼二阶系统，闭环传递函数写出来就是个震荡环节，公式当然还是前面的就没问题

\[\begin{array}{} \left\{ \begin{align} \omega_r &= \omega_n \sqrt{1 - 2 \xi^2} \\ M_r &= \frac{1}{2\xi\sqrt{1 - \xi^2}} \\ \end{align} \right. \end{array}\]

• 带宽频率

特别注意这是在闭环上定义的。

以零频值为准，往下0.707倍对应的频率就是带宽频率。认为小于带宽频率的信号，经过闭环系统可以很好的通过，有点低通滤波器的意思，带宽说明了通过信号的能力，带宽越宽响应越快越迅速。

对于一阶系统\(\Phi(s) = \frac{1}{Ts + 1}\)

\[\omega_c = \omega_b\]

到这里要仔细区分好开环还是闭环了。

闭环频域指标和时域指标也是有关系的，对于二阶系统，可以精确的算出来，虽然略微复杂：

\[\begin{array}{} \left\{ \begin{align} M_r &= \frac{1}{2\xi\sqrt{1 - \xi^2}} \\ \omega_b &= \omega_n \sqrt{ 1 - 2\xi^2 + \sqrt{ 2 - 4\xi^2 + 4\xi^4 } } \end{align} \right. \end{array}\]

相应地，高阶系统也可能会有谐振，在\(1 \le M_r \le 1.8\)的情况下，前辈又总结好了：

\[\begin{array}{} \left\{ \begin{align} \sigma\% &= \left[ 0.16 + 0.4 \left( M_r - 1 \right) \right] \times 100\% \\ t_s &= \frac{\pi}{\omega_c}\left[ 2 + 1.5 \left( M_r - 1 \right) + 2.5\left( M_r - 1 \right)^2 \right] \end{align} \right. \end{array}\]

实际物理系统闭环带宽频率和开环截止频率的数量级差不多，基本差不多，实际算的时候，如果代带宽频率也差不多。