李雅普诺夫稳定性分析

*13）正确理解李雅普诺夫稳定性的有关概念； 14）掌握李雅普诺夫第二法，初步掌握寻求系统李雅普诺夫函数判定系统稳定性的方法。

stability

Lyapunov

注意这个定语，不是"线性系统"了，是范围更大的"控制系统"。

到了现代控制理论的这里，"稳定"有了精确的数学定义和不同的稳定状态。前面经典控制里面我们认为系统最后靠近一个值就是稳定的（粗略的讲）。现在遇到的问题是比如极限环自振，说他不稳吧，他和那种系统跑飞崩溃还不一样，说他稳吧，这还在动。所以有了稳有了不同的稳法。

关于稳定的一些提法，最核心的是：李雅普诺夫稳定性、渐进稳定性、大范围渐进稳定。还有像极限定义一样的对稳定的数学描述。

当然稳定不是为了玩弄概念，我们是为了在拿到一个控系统系统后，研究其最根本的稳不稳问题。稳了再谈后面设计校正优化的事情。

李雅普诺夫建立了基于状态空间描述的稳定性理论，提出了依赖于线性系统微分方程的解来判断稳定性的第一方法(称为间接法〉和利用经验和技巧来构造李雅普诺夫函数借以判断稳定性的第二方法(称为直接法)。

李雅普诺夫提出的这一理论是确定系统稳定性的更一般的理论，不仅适用于单变量，线性﹑定常系统，还适用于多变量、非线性、时变系统。

各种稳定性的定义

这里的稳定针对的系统可以上升到非线性时变的情况。系统的状态方程：

\[\boldsymbol{\dot{x}} = \boldsymbol{f}(\boldsymbol{x},t)\]

首先要想想平衡状态（平衡点）该怎么用数学表达呢？状态不再随时间运动就是平衡了，数学表达就是

\[\boldsymbol{\dot{x_e}} = \boldsymbol{f}(\boldsymbol{x_e},t) = \boldsymbol{0}\]

从一个高中物理的小例子出发，一个滑块在圆弧轨道里运动的问题。

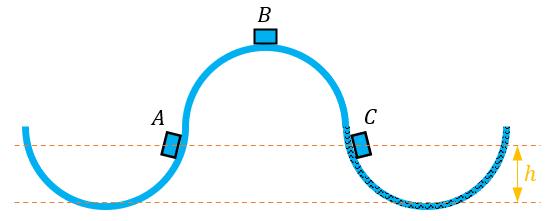
滑块A的轨道光滑，可以想想A一直做来回运动，永不停止。滑块B绝对是不稳的，只要动一下就回不到平衡点了。滑块C的轨道是有摩擦力的，最终能量消耗完了，就停在最低点了，就是稳定点。

分别对应了李雅普诺夫意义下的稳定、不稳定、大范围渐近稳定。

李雅普诺夫稳定性

状态空间轨迹在稳定点的附近运动。

系统做不衰减的震荡也可以认为是稳定的。或者稳定极限环。

数学定义和极限很像，不过状态空间里的抽象距离，用范数取讲这个事情

\(\Vert \Vert\)，敲公式太麻烦了。后面有空在说吧。

总之这个数学定义相当严谨的，要求状态初始点在状态空间里距离稳定点不远，时间往大走，状态点都离稳定点不远，大概就这么个事情。

要求初始点这个事情在全局稳定里就理解为啥这里要这个前提了。

对于非线性系统，李雅普诺夫稳定性可以进行一阶近似丢掉高阶项进行分析，因为讲的是领域嘛，可以这么搞。而且很合理。稳定点线性化九的就是领域的事情，李雅普诺夫稳定也是讲的领域的事情，这就正好对上了。

渐近稳定性

状态空间轨迹最终停在平衡点了。经典控制理论里面的稳定全是渐近稳定。

也可以看出渐进稳定，首先得李雅普诺夫稳定。并且要求最后状态点就停在稳定点了，当然也包含了状态初始点在稳定点附近这个前提。

大范围渐进稳定性

整个状态空间，不管状态初始点在哪里，轨迹都能运动到平衡点。

非线性系统稳定和初始值也有关系（具体可以随便拿个相图看看），线性系统倒是只和结构有关。这里稳定性是针对所有系统去谈，所以前面强调初始点要离平衡点不远，如果任意初始点，那就是大范围稳定了。

在前面非线性系统，用二阶相图近似分析的时候，体会一下。

BIBS稳定性

任意有界的初始状态，在任意有界的输入下，状态均有界

线性定常系统，BIBO判断主要依据系统矩阵A，特征值在左半开平面，则BIBS稳定。

BIBO稳定性

任意有界的初始状态，在任意有界的输入下，输出均有界

线性定常系统，BIBO判断主要依据传递函数，极点在左半开平面，则BIBO稳定。

对于线性定常系统，如果渐进稳定，则必然BIBS稳定，BIBO稳定。

但是如果李雅普诺夫稳定，系统不一定BIBS稳定，BIBO稳定。

李雅普诺夫稳定性间接判别法

第一法是用状态方程的解来判断系统稳定性的方法。

对于线性系统\(\dot{x} = Ax\)来讲线性定常系统的特征值判据：系统矩阵A的全部特征值在复平面左半部。

这是渐近稳定充要条件：

\[Re(\lambda_i) \leq 0 \ \ \ \ (i=1,2,\cdots,n)\]

即系统矩阵A的全部特征值位于复平面左半部。这个经典理论相通。

对于非线性系统来说，首先可以使用线性化的手段。实际上在前面非线性分析里已经有过这个行为了。用二阶系统相图近似分析平衡点稳定性。

因此，对于非线性系统的稳定性分析，先考虑如何进行线性化。一元函数经典泰勒。二元也是，二元泰勒

\[\begin{array}{} \left\{ \begin{align} \dot{x_1} &= f_1(x_1,x_2) \\ \dot{x_2} &= f_2(x_1,x_2) \\ \end{align} \right. \end{array}\]

先得找到平衡点，毕竟是在平衡点附近做线性化。如果平衡点在\(x_e = (x_1,x_2) =(0,0)\)

那么线性化之后的系统矩阵就是

\[\boldsymbol{A} = \left[\begin{array}{c} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} \end{array}\right]\]

线性化是在平衡点的邻域进行的，因此这个方法只能看出局部稳定性，也即李雅普诺夫稳定性，没法推出全局稳定，区别于线性定常系统的极点稳定性情况。

使用这个方法判断的时候还有个问题，遇到了线性化特征值为0的情况，这个情况不知道稳不稳，因为线性化忽略了高阶项，一阶线性部分遇到了0，稳定性是由被忽略的高阶项决定的。

李雅普诺夫稳定性直接判别法

用李雅普诺夫函数\(V(\boldsymbol{x},t)\)（广义能量函数，标量函数）直接对平衡状态稳定性进行判断，不用求出系统状态方程的解。各种系统全能用，很猛。

这时候再拿过来前面那个滑块运动的小例子，来理解一下这个方法大概的思想

根据物理学原理，系统存储的能量（动能和势能）随着时间而衰减，那么系统迟早会达到一个不动的平衡的状态。滑块轨道有摩擦，最后滑块停在最低点。大概思路就是这样，但是实际的人造物理系统的能量函数很难找，李雅普诺夫引入了广义能量函数。

至今没有通用的构造李雅普诺夫函数的方法，所以，做题就是在积攒经验。

• 大范围渐进稳定： 若 \(V(\boldsymbol{x})\) 正定，\(\dot{V}(\boldsymbol{x})\) 负定，当 \(\Vert \boldsymbol{x} \Vert \to \infty\)时， \(V(\boldsymbol{x}) \to \infty\)。

则平衡状态时大范围渐进稳定的。

这个含义是，能量肯定是大于零的，但是能量是衰减的，所以最后能量衰减完了就不运动了。这就是渐进稳定了。这就是滑块C的情况。

根据这个思路，不管什么情况能量肯定都是大于零的，不会有负能量出现，来看看能量的变化率即\(\dot{V}(x)\)的情况

\(\dot{V}(x)\)负半定，非零状态不恒为0，那么也渐近稳定。这个意思是说，我可以偶尔不衰减，但是最终能量到到0。

\(\dot{V}(x)\)负半定，非零状态恒为0，那么李雅普诺夫稳定。系统最终能量减小到一个数了，等幅运动了。

\(\dot{V}(x)\)正定，不稳定。这没的说，能量居然越来越大了。

这个有点意思，看起来是随便找个函数让他正定，他的导数负定，就能确定稳定性呢。但实际上是用能量去判断的，一个系统能量是正的，但是能量是衰减的，最终能量没了，就不跳了，稳定了。这个思路很有借鉴意义，在倒立摆起摆控制也有这种思路，让倒立摆的机械能变大，就立起来了。

然后问题又来了，这个能量函数又该怎么找呢？坏消息是没有构造李雅普诺夫函数的通用方法，一个字：凭感觉。

这个条件是偏保守的，也就是说第二法是充分条件，满足必稳定，但是稳定不一定都满足。

前面是随便一个系统找函数，到了线性系统里，有结论了。

一个线性系统的状态方程为\(\boldsymbol{\dot{x} = Ax}, \boldsymbol{x}(0) = \boldsymbol{x}_0\) ，系统矩阵非奇异，原点是唯一平衡点。

假设取的正定二次型能量函数为\(V(\boldsymbol{x}) = \boldsymbol{x}^T\boldsymbol{Px}\)，如果这个函数是存在的，那么

\[\dot V(\boldsymbol{x}) = \boldsymbol{\dot x}^T\boldsymbol{Px} + \boldsymbol{x}^T\boldsymbol{P\dot x}\]

带入状态表达式

\[\dot V(\boldsymbol{x}) = \boldsymbol{x}^T\boldsymbol{A}^T\boldsymbol{Px} + \boldsymbol{x}^T\boldsymbol{PAx} = \boldsymbol{x}^T(\boldsymbol{A}^T\boldsymbol{P} + \boldsymbol{PA})\boldsymbol{x}\]

令 \(-\boldsymbol{Q} = \boldsymbol{A}^T\boldsymbol{P} + \boldsymbol{PA} \tag{*}\)

于是线性定常连续系统稳定的充要条件：给定一正定矩阵\(\boldsymbol{P}\)，存在满足*式的正定矩阵\(\boldsymbol{Q}\)

*式叫李雅普诺夫矩阵代数方程。

实际使用的时候先给Q为I，看能不能求出P是正定的。

对于线性系统有标准化的判断方法，但是对于非线性，使用这个能量函数去判断还是不容易的，这个能量函数的找法没有通用的方法，很难搞。

克拉索夫斯基提出的构造非线性李雅普诺夫函数的方法

还有个变量梯度法。

多举个例子，感受一下李雅普诺夫直接法的标量函数时怎么找的

非线性系统的状态方程

\[\begin{array} {} \dot{x_1} = x_2 - x_1 ( x_1^2 + x_2^2 ) \\ \dot{x_2} = -x_1-x_2 ( x_1^2 + x_2^2 ) \end{array}\]

平衡状态，求出来x1=0，x2=0。

\[V(x) = x_1^2(t) + x_2^2(t)\] \[\dot{V}(x) = 2x_1\dot{x_1} + 2x_2\dot{x_2} = -2(x_1^2 + x_2^2)^2\]

注意这是个对t的函数，链式法则求导。