离散系统的分析
分析,即稳定性,稳态误差,动态性能。
稳定性
有了数学模型,又要执着的证明稳不稳了、什么情况下稳了。毕竟这是应用数学,不证明不专业,不像是个搞理论的。
前面简单的提了一下z变换表面上看是做了个代换\(z = e^{Ts}\)

可以看出虚轴是映射到z平面单位圆了,稳定区域到单位圆里面了。
主带映射为整个z平面,满足采样频率的情况下,所有零极点都是落在主带里的。次要带就不管了。
这种映射有个小问题是,左半平面映射到单位圆里,数据密度过高,所有要求的计算精度比较高
当然还是要严格证明一下
\[\Phi(z) = \sum_{j=1}^n \frac{ C_jz }{z - \beta_j}\]由稳定性的定义,单位脉冲响应的最终输出为0,也就是说\(\Phi(z) = C(z)\),要求\(c(k) = 0\)
\[k \to \infty, c(k) = \sum_{j=1}^n C_j \beta_j^k = 0\]那么\(\mid \beta_j \mid < 1\),也就是说,极点的模小于1.
定理是这么个定理,但是用起来不方便。为了使用的方便,做一个双线性变换把z平面映射w平面,使得判断方法和在z平面的判断方法一样。这时候就可以直接用s平面的劳斯判据了。劳斯判据再数学上是判断根的实部的位置,但是在控制理论里有了稳定这一层的含义。因此这个方法和字母没有关系,映射之后方法是通用的。
但是为啥s映射到z又映射到w呢,这个w和一开始的s啥关系呢?由多对一再到一对一映射,实际上相当于把s的主要带映射到整个w平面了。
双线性变换
\[\begin{array}{} \left\{ \begin{align} z &= \frac{w+1}{w-1}\\ w &= \frac{z+1}{z-1}\\ \end{align} \right. \end{array}\]这个映射使得z平面的单位圆映射为w的虚轴。
这时候用Routh判据没有任何问题。
然后又有人觉得做个映射还不是很方便,能不能直接研究z平面的特征多项式,像劳斯判据一样直接用系数来判断根在不在单位圆里稳定性,这就有了朱利(Jurry)判据。
这反正也是个纯数学工具,就考试来讲记住用就完事了。
举个例子,忘记的时候回来复习(关键词:朱利判据例题)
\[D(z) = -39 + 119z -117z^2 + 45z^3 = 0\]首先\(D(1) > 0\),\(D(-1) < 0\),最高次数是3,要小于0。这个先要满足,然后列出jurry表。
| Jurry | \(z^0\) | \(z^1\) | \(z^2\) | \(z^3\) |
|---|---|---|---|---|
| 1 | \(-39\) | \(119\) | \(-117\) | \(45\) |
| 2 | \(45\) | \(-117\) | \(119\) | \(-39\) |
| 3 | \(b_0\) | \(b_1\) | \(b_2\) | |
| 4 | \(b_2\) | \(b_1\) | \(b_0\) |
最后剩3列停下,第一列拿出来,加上绝对值
\[\vert -39 \vert \color{red}<\color{black} \vert 45 \vert > \vert -504 \vert > \vert -792 \vert >\]条件都满足,那么就是稳定的。
除了双线性变换用Routh判据和直接用Jurry判据,还有个很经典的根轨迹。
根轨迹拿掉物理上的应用,从纯数学的角度讲就是分析根随参数的变化的。因此,同样是复数方程,自然也可以使用同样的方法画出根轨迹,只不过字母变成了z。
但是这里注意分析稳定性的时候,不再是复平面左半边了,是单位圆内部了。用几何方法算出来各种参数,基本的思路大概就是这样。
稳态误差
稳态误差也可以参考连续系统,基本思路是相同的,前面那么长的z变换数学铺垫,就是为了使用连续系统里相同的思路。
最很根本的是终值定理,误差传递函数来计算,后面的都是这个衍生出来的二级结论,这些也是从连续系统的思想里来的,不过用的是离散工具,把握住最根本的,后面的可以推出来的。
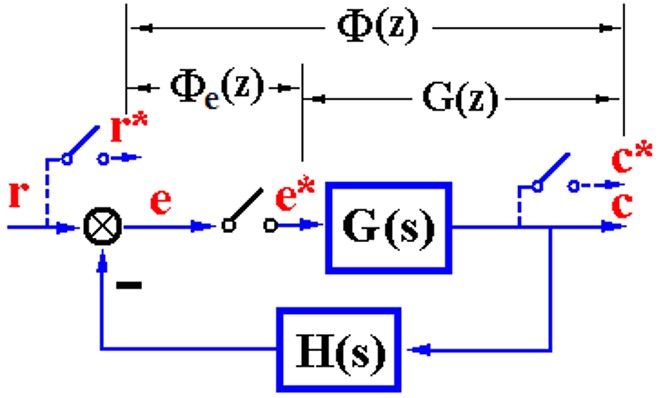
这里为啥积分环节变成了(z-1),因为\(z = e^{Ts}\),映射关系。
\[\lim_{z \to 1} GH_0(z) = K\]这个也是从连续来的。这里甚至都没有写开,也不用写开。
那么误差脉冲传递函数
\[\Phi_e(z) = \frac{1}{1 + GH(z)}\]使用最根本的终值定理
\[e(\infty) = \lim_{z \to 1}(z-1)\Phi_e(z)R(z) = \lim_{z \to 1}(z-1)\frac{1}{1 + GH(z)}R(z)\]后面还是全部使用连续的思想,离散的工具
阶跃输入\(R(z) = A\frac{z}{z-1}\)
\[e_{ssp}(\infty) = \lim_{z \to 1}(z-1)\frac{z}{z-1}\frac{1}{1 + GH(z)} = \frac{1}{1 + \lim_{z \to 1}GH(z)} = \frac{1}{1+ K_p }\]斜坡输入\(R(z) = A\frac{Tz}{(z-1)^2}\)
\[e_{ssv}(\infty) = \lim_{z \to 1}(z-1)\frac{ATz}{(z-1)^2}\frac{1}{1 + GH(z)} = \frac{AT}{\lim_{z \to 1}(z-1)GH(z)} = \frac{AT}{K_v }\]加速度输入\(R(z) = \frac{A}{2}\frac{T^2z(z+1)}{(z-1)^3}\)
\[e_{ssa}(\infty) = \lim_{z \to 1}(z-1)\frac{A}{2}\frac{T^2z(z+1)}{(z-1)^3}\frac{1}{1 + GH(z)} = \frac{AT^2}{\lim_{z \to 1}(z-1)^2GH(z)} = \frac{AT^2}{K_a }\]这几个系数和连续是一个意思,但是有一点不同的是,和采样周期也有关系了,这点很有意思。注意这个系统是一拍一拍脉冲直接冲击这个系统。
从这里也能看出一点点采样对系统的影响,采样周期越大,稳态误差越大。
总结一下,离散系统,没有ZOH的时候,稳态误差
\[K_p = \lim_{z \to 1}G(z)\] \[K_v = \lim_{z \to 1}(z-1)G(z)\] \[K_a = \lim_{z \to 1}(z-1)^2G(z)\] \[e_{ssp} = \frac{A}{1+ K_p }\] \[e_{ssv} = \frac{AT}{K_v}\] \[e_{ssa} = \frac{AT^2}{K_a}\]为了说明这个"一拍一拍"冲击的含义,举个例子
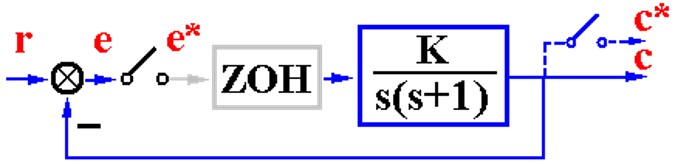
输入为\(2t\),讨论有无零阶保持器对系统的影响
没有ZOH就很简单了
\[GH(z) = \frac{K(1-e^{-T})z}{(z-1)(z-e^{-T})}\] \[K_v = \lim_{z\to 1}(z-1)GH(z) = K\] \[e_{ssv}(\infty) = \frac{AT}{K}\]可以看出稳态误差和T有关系的,当然咳哟古额稳定性的问题,在连续系统里G(s)不论K大小都稳定,想象一下根轨迹。离散了以后就不一定了,系统稳定性后面说。
有了ZOH
\[G(z) = \mathscr{Z} \left[ \frac{1 - e^{-Ts}}{s} \cdot \frac{K}{s(s+1)} \right] =\] \[K_v = \lim_{z\to 1}(z-1)GH(z) = KT\] \[e_{ssv}(\infty) = \frac{AT}{KT}\]可以看出,加了ZOH,稳态误差和连续系统的表达是一样的。
再来说一下离散对稳定性的影响
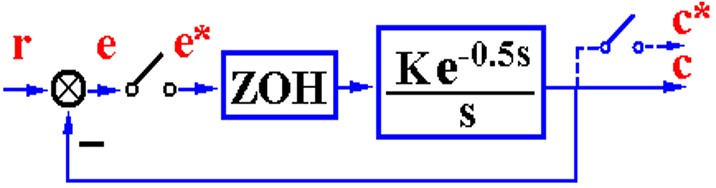
先得找出开环脉冲传递函数,然后有特征多项式,最后Jurry判据。这个系统有个纯延时环节
\[G(z) =\]同样的,也有动态误差系数来看误差的稳态分量。
把误差脉冲传递函数进行幂级数分解,输入
动态性能
参考连续系统,典型二阶欠阻尼,极点对系统性能的影响。
\[\Phi(z) = \frac{M(z)}{D(z)} = K^*\frac{\prod \limits_{i=1}^m(z-z_i)}{\prod \limits_{j=1}^n(z-p_j)}\]研究极点对应的模态。写成上面这种形式,已经写成闭环形式了。在阶跃作用下来看这个系统的情况
\[C(z) = K^*\frac{\prod \limits_{i=1}^m(z-z_i)}{\prod \limits_{j=1}^n(z-p_j)}\cdot \frac{z}{z-1} = \frac{M(1)}{D(1)}\cdot \frac{z}{z-1} + \sum \frac{C_iz}{z-p_i}\]前面一项是阶跃响应的稳态分量,前面那个是增益。后买你则是一堆极点的瞬态分量,模态对应的响应为
\[c_i^*(t) = \mathscr{Z^{-1}} \left[ \frac{C_iz}{z-p_i} \right]\]则\(c_i(kT) = C_ip_i^k\)
这个就是单个模态,根据p很容易就能想象这个情况
在实轴上,模大于1,自然发散,小于1收敛。如果是负数,那么就是正负来回跳动,发散情况还是由模长决定
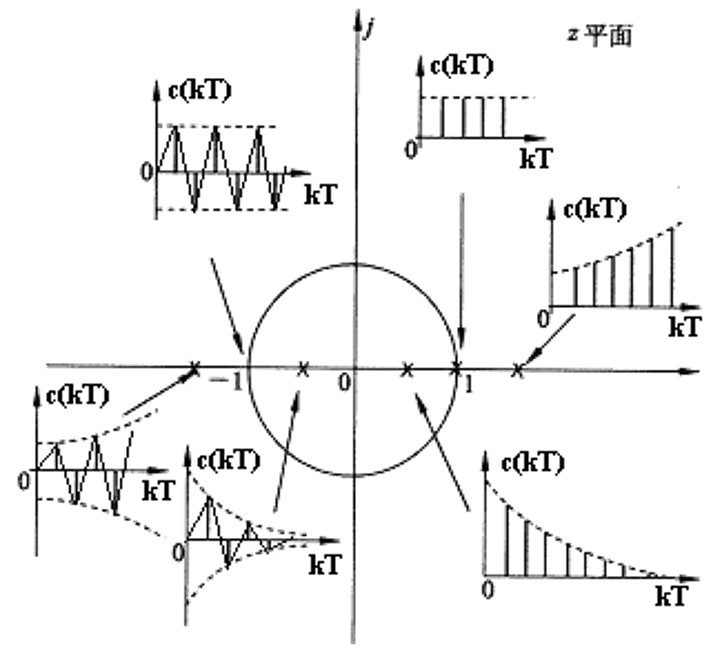
还是很容易对应起来的。
交替变换,叫成离散系统的振铃现象。
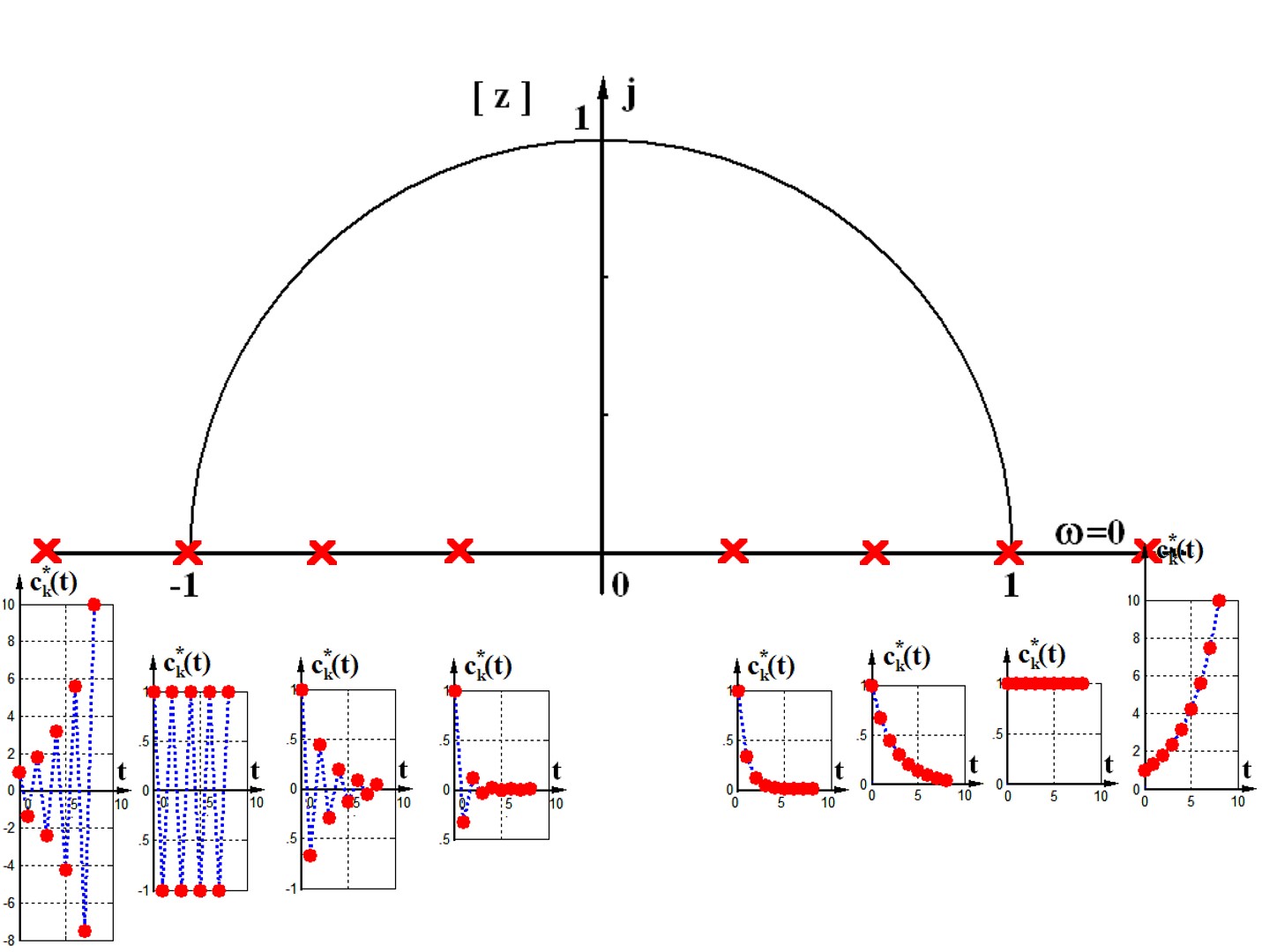
上面是单实根,如果是共轭复根,想看最根本的
\[c_{i,i+1} = \mathscr{Z^{-1}} \left[ \frac{C_iz}{z-p_i} + \frac{C_{i+1}z}{z-p_{i+1}} \right] = C_ip_i^k\]经过一串推导,总之又换成三角函数了,还是一样的,复数引入震动。在离散这里,包络线是三角函数,还有个一个周期几拍的问题。
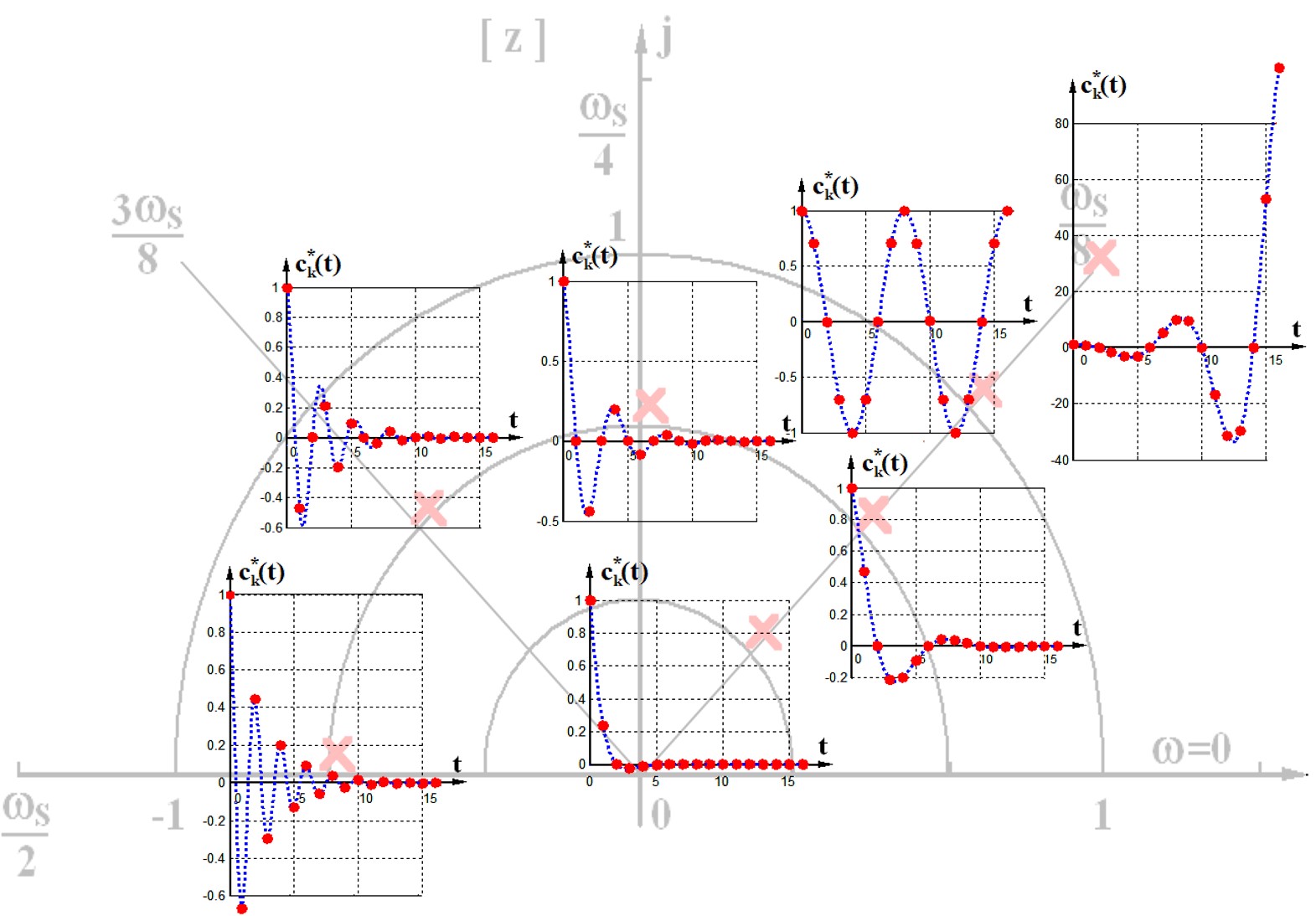
抓住根本(根本表达还没写出来),模长决定了收敛发散,模长越小,收敛越快,角度决定了频率。
定性的结论大概就是这么个样子。
真要去分析的话,求系统脉冲传递函数,求C(z),反变换,就可以精确的确定每个时间点的响应,和各种指标了。
还是前面分析稳态误差那个系统

K=1,分析超调量,调节时间
没有ZOH时候
\[G(z) = \mathscr{Z} \left[ \frac{K}{s(s+1)} \right] = \frac{K(1-e^{-T})z}{(z-1)(z-e^{-T})}\]则
\[\Phi(z) = \frac{G(z)}{1+G(z)} = \frac{0.632z}{z^2 - 0.736z + 0.368}\] \[c(\infty) =\]一般来说,这分解因式解根属实不容易,那么就除就完事了,找个足够多的拍数,精确响应直接就看出来了。
加上ZOH再来一下这个过程
\[G(z) = K(1-z^{-1}) \mathscr{Z} \left[ \frac{1}{s^2(s+1)} \right] = 不会算\]对于这个也可以画根轨迹,画法还是原来的画法,但是稳定边界是单位圆了。
最后对于最终不稳定的系统,也可以用动态误差系数法找出误差的稳定分量。
