可控性和可观性
Controllability, Observability
- *6)正确理解可控性、可观测性的基本概念;
- *7)熟练掌握判定系统的可控性、可观测性充要条件及有关方法;
- 8)理解可控性、可观测性与系统传递函数的关系;
可控可观的理解
经典控制理论里,没有提过这个事情。因为经典控制里的东西,输出量好像就是直接被传感器测量的,而且输出就是要被控制的。放在这个语境里经典控制系统的输出量既可观又可控。
但用状态方程可输出方程描述系统的时候,除了最终的输出量,还有系统内部变量。这时候就有了内部状态是否都可以被输入影响和输出能否反映所有内部状态的问题。
可控性和可观测性的问题。
(举例子。。)
下面讲的不好。。将来优化。
能控性能观性属于承上启下的章节,考虑到涉及的概念和定理很多,篇幅较长,因此将传统的这一章分成了能控能观的介绍和规范形与结构分解。但从逻辑上这两部分是紧密联系的
研究可控可观是为了干什么?
从工程应用角度来说,能控性和能观性如此重要是因为他还与许多问题的可解性有关。比如极点可否任意配置,LQR控制,Kalman滤波的稳定性,H∞控制等都与能控能观性有密切关系。这里多说一句,卡尔曼引入状态空间法也不仅仅是单纯为了分析系统,在状态空间方法有一个最著名的推论:若状态空间方程能控,则状态反馈可以实现任意的特征值配置,如果状态空间方程能观,则可以构造出具有任意期望特征值的状态估计器。
举个简单例子
\[\begin{array}{} \left\{ \begin{align} \dot{x_1} &= 2x_1 + 3u \\ \dot{x_2} &= 4x_2 \\ y &= x_2 \end{align} \right. \end{array}\]输入u很显然可以影响x1,输出y显然反映x2,为啥可控可观重要呢?
\[x_2(t) = e^{4t} \cdot x(0)\]这个状态,因为这个4,发散了,同理这个如果是负数,是不是就稳定了。
那么可以看出\(x_1\)也不稳定,但是如果我让输入为\(-x_1\),是不是这个状态就变成了
\[x_1(t) = e^{-t} \cdot x_1(0)\]这个状态是不是就稳定了。要想实现这个东西,我得知道x1,因此我得知道\(x_1\)才能实现这个事情。可观才能观察到状态然后反馈到输入,可控才能控制状态。
即对角矩阵,输入矩阵只要没有为0,那么状态都可控。
对角阵的可控与可观
对角阵是我最喜闻乐见的矩阵,最适合当坐标系。有着优秀性质。
在控制里,如果是对角阵,一样就能看出系统的状态是否可控。甚至都说不出为啥可控,上面那上面这个简单小例子实际上是系统矩阵为对角阵的一个判据。
更一般的
\[\left [ \begin{array}{c} \dot{x_1} \\ \dot{x_2} \\ \dot{x_3} \\ \end{array} \right ] = \left [ \begin{array} {c} a_1 & 0 & 0 \\ 0 & a_2 & 0 \\ 0 & 0 & a_3 \end{array} \right ] \left [ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right ] + \left [ \begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \end{array} \right ]u\] \[y = \left [ \begin{array} {c} c_1 & c_2 & c_3 \end{array} \right ] \left [ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right ]\]用状态变量图来看看
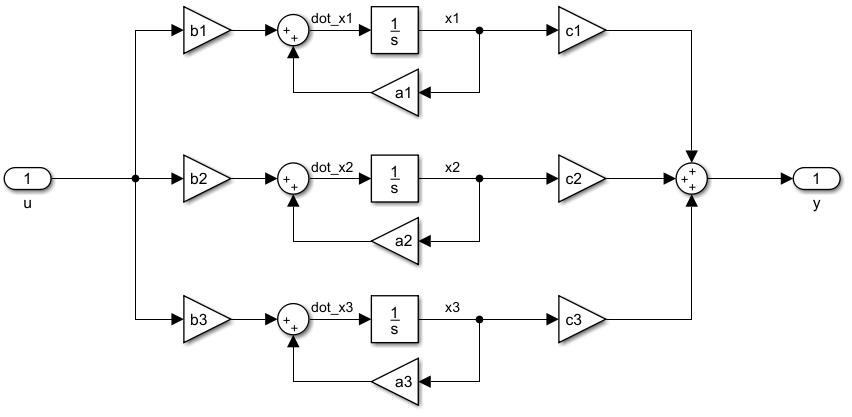
如果某个\(b_i = 0\)那么就会有一部分无法控制
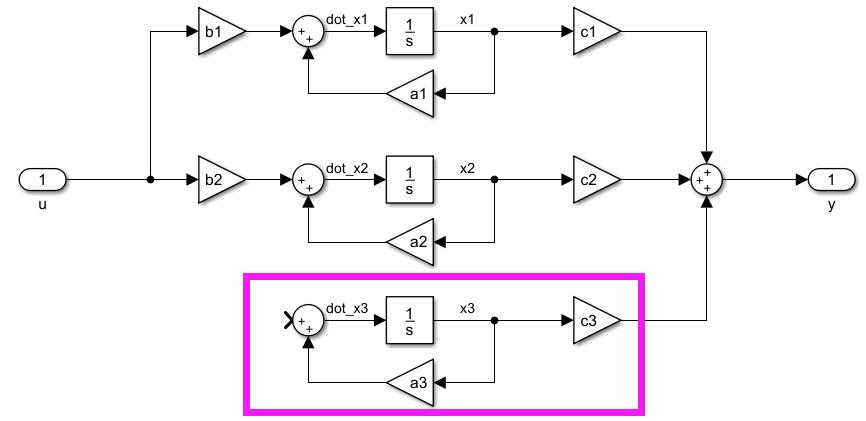
如果某个\(c_i = 0\),那么就有一部分无法通过输出\(y\)体现出来
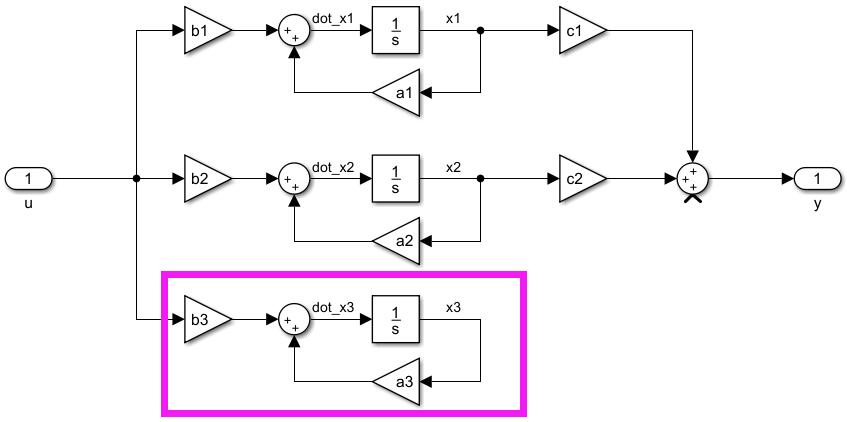
最完蛋的情况就是不可控不客观,状态图有一部分直接悬空,这种情况就比较难搞。
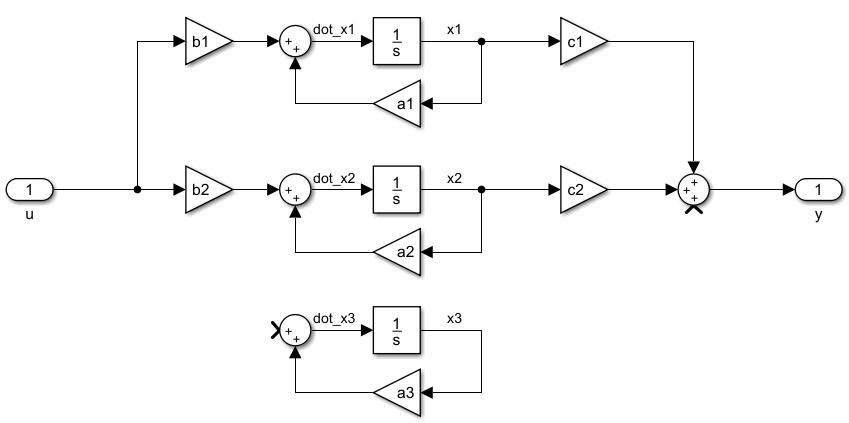
上面就是对角阵的可观可控判据。
约当阵的可控与可观
不幸的是,有一部分矩阵对应的相同特征值仅有一个无关的特征向量,这种情况下,矩阵无法相似对角化。但是可以变成约当阵。
约当阵没有对角阵那么好,但是也大差不差吧,能用。
约当阵举个例子
\[\left [ \begin{array}{c} \dot{x}_{11} \\ \dot{x}_{12} \\ \dot{x}_{13} \\ \hdashline \dot{x_{4}} \\ \end{array} \right ] = \left [ \begin{array} {ccc:c} a_1 & 1 & 0 & 0\\ 0 & a_1 & 1 & 0\\ 0 & 0 & a_1 & 0 \\ \hdashline 0 & 0 & 0 & a_4 \end{array} \right ] \left [ \begin{array}{c} x_{11} \\ x_{12} \\ x_{13} \\ \hdashline x_{4} \\ \end{array} \right ] + \left [ \begin{array}{c} b_{11} \\ b_{12} \\ b_{13} \\ \hdashline b_4 \\ \end{array} \right ]u\] \[y = \left [ \begin{array} {ccc:c} c_{11} & c_{12} & c_{13} & c_{4} \end{array} \right ] \left [ \begin{array}{c} x_{11} \\ x_{12} \\ x_{13} \\ \hdashline x_{4} \\ \end{array} \right ]\]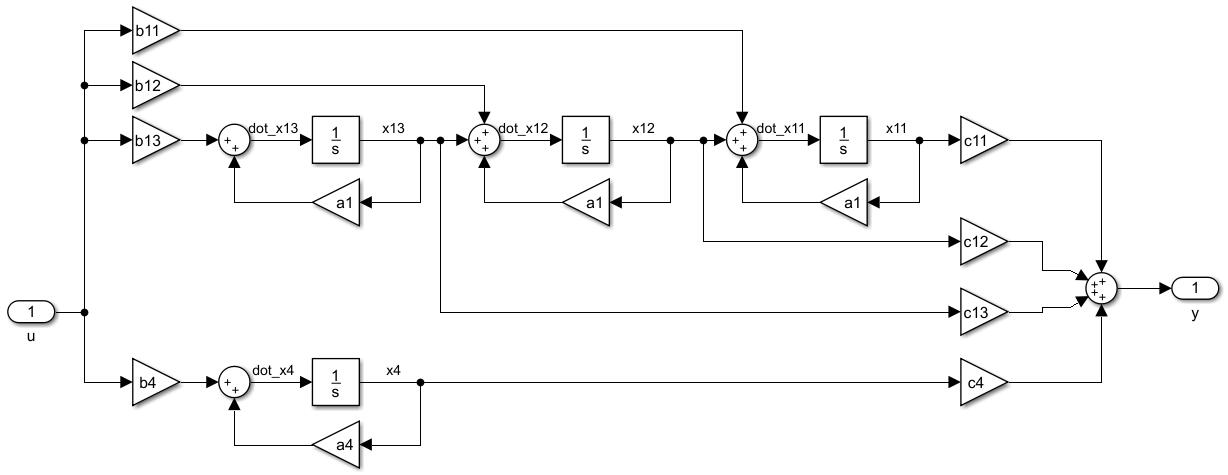
可以看出,约当块以外的部分判断和对角阵一样,约当块是串联到一起的,因此关注最前面的东西。也就是约当阵判据比较关注约当块对应B阵的最后一行。对应状态图里站在最前面的那个状态的输入,反正后面都串在一起,直管排头,后面跟着就可以控制了。
相应的,可观性,只看队尾那个状态就行,因此判据关注约当块对应的C阵的第一列。
遇到相同特征值的约当块,为了直击本质,取一个特殊的约当阵,由前面知道了每个约当块的可控性只看状态图排头的那个输入就行,因此中间的变量的输入系数就取0,这样简化下来,每个单独的约当块一定是可控的,但是看看相同特征值的约当块组合起来会由什么问题
\[\left [ \begin{array}{c} \dot{x}_{11} \\ \dot{x}_{12} \\ \hdashline \dot{x}_{21} \\ \dot{x}_{22} \\ \end{array} \right ] = \left [ \begin{array} {cc:cc} 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \hdashline 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right ] \left [ \begin{array}{c} x_{11} \\ x_{12} \\ \hdashline x_{21} \\ x_{22} \\ \end{array} \right ] + \left [ \begin{array}{c} 0 \\ 1 \\ \hdashline 0 \\ 1 \\ \end{array} \right ]u\] \[y = \left [ \begin{array} {cc:cc} 1 & 0 & 1 & 0 \end{array} \right ] \left [ \begin{array}{c} x_{11} \\ x_{12} \\ \hdashline x_{21} \\ x_{22} \\ \end{array} \right ]\]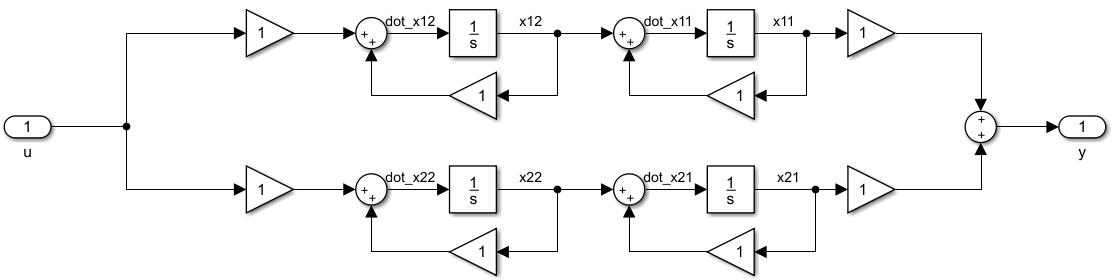
凭借着对图的朴素感情和直观理解,好像上面的一块是可控可观的,下面的一块也是可控可观的。确实单独看是这样,但是如果仔细看看,会发现下面的不就是上面的完整复制了一份,只是状态变量变了个名字而已。
那么这时候还能叫状态可控吗?借用线性代数的话术说,这是不是就是线性相关的,在一个输入的作用下,这两部分没法自己变化自己的,所以这也是一种不可控,和前面一部分悬空的不可控不一样。
这种不可控是一部分会随着另一部分变化,这也是比较难搞的一种情况。
然后看可观性,其实思路是一样的,如果说为啥不把输出/2就能得到每个块的输出呢,这个问题就和为啥不把输入信号幅值*2一样。这是个特殊的例子,实际情况下,这个比例值不同,积分环节数不同,但是都是可以从这个简单的角度去理解。用特殊去理解一般,前面的东西可能说的不太精准,但是我觉得还是比较通俗的。
那么该如何操作才能使得系统可控呢,这个问题实际上就是输入维数和可控性的关系。首先至少要有两个输入,才有可能使得系统可控,使得上下两部分自己走自己的。
\[\left [ \begin{array}{c} \dot{x}_{11} \\ \dot{x}_{12} \\ \hdashline \dot{x}_{21} \\ \dot{x}_{22} \\ \end{array} \right ] = \left [ \begin{array} {cc:cc} 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \hdashline 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array} \right ] \left [ \begin{array}{c} x_{11} \\ x_{12} \\ \hdashline x_{21} \\ x_{22} \\ \end{array} \right ] + \left [ \begin{array}{c} 0 & 0 \\ 1 & 0 \\ \hdashline 0 & 0 \\ 1 & 0 \\ \end{array} \right ] \left [ \begin{array}{c} u_1 \\ u_2 \\ \end{array} \right ]\]继承前面的思路,两个输入还是只操作排头的就行,最最最朴素的情感告诉我,上面部分一个单独输入,下面一个单独输入,这个系统一看就上下部分可以自己管自己。这一看就太可控了。然后两个输出,上面单独出下面单独出。
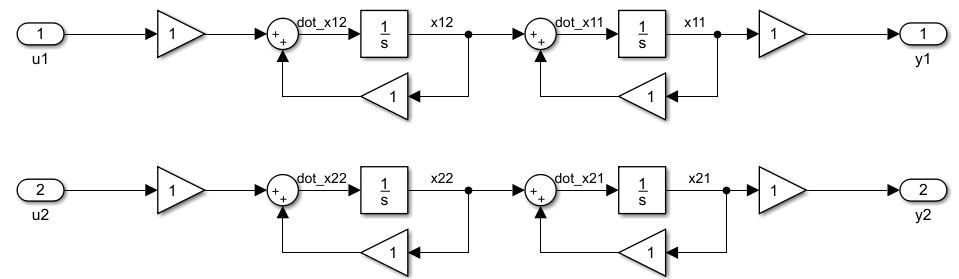
这就相当于一个拆两个,这才是真正意义上的,每个单独的约当块都可控可观。每个单独的约当块都像是一个独立的系统,互不干扰,也没有变化相关这一说。
到目前为止,全是直观感觉,还没有用到基础数学知识,接下来要向考虑更加一般的情况了。
两个输入有交叉,在一种特殊情况下和一个输入的效果相同,数学上叫"线性相关",大多数情况下虽然有交叠,但是也是可控的,这就是判据里的最后一行向量无关,系统可控的说法。
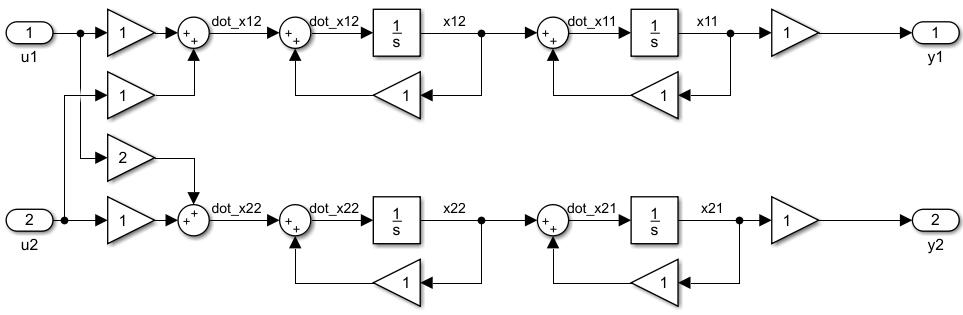
从抽象空间的角度考虑,一个输入是一个基,两个无关输入就是一个输入空间,输入部分是一个矩阵变换,如果变换时非奇异的,那么输入空间经过变换以后不降维,如果输入部分相关了,这两个输入可一个输入一样。
上面这么一堆,就是约当阵的可控性判据,做题的时候就两句话:
每个约当块末行对应的B的行向量不为全零行。
同一特征值的不同约旦快末行对应B的行向量无关。
一般矩阵的可控与可观
更不幸的是,一般系统矩阵就是个普通形式的,就很难搞。
通过矩阵变换和以获得对角阵和约当阵,这是一个方法。而且有很直观的意义。
但是更多的情况时不想做变换,能不能直接通过一些运算,最好是简单一点的运算,起码比做变换简单的运算就能知道系统可控可管的情况。这个思路其实和劳斯判据一样,为了使用简单搞出来的数学方法。甚至名字都有相似的地方,叫做判据。
可控性判据
\[\boldsymbol{S} = \left[\begin{array}{c} \boldsymbol{B} & \boldsymbol{AB} & \cdots & \boldsymbol{A^{n-1}B} \end{array}\right]\] \[\boldsymbol{V} = \left[\begin{array}{c} \boldsymbol{C} \\ \boldsymbol{CA} \\ \vdots \\ \boldsymbol{CA^{n-1}} \end{array}\right]\]若可控可观,那么
\[rank\boldsymbol{S} = rank\boldsymbol{V} = n\]这是最一般的,随便拿来个什么系统,都能这么判断。
还有个输出可控性判据
\[\boldsymbol{S}_0 = \left[\begin{array}{c} \boldsymbol{CB} & \boldsymbol{CAB} & \cdots & \boldsymbol{CA^{n-1}B} & \boldsymbol{D} \end{array}\right]\] \[rank\boldsymbol{S}_0 = q\]q是输出维数
总结
- 格拉姆矩阵判据,
- 秩判据,
- PBH判据,
- 对角规范型判据,
- 约当规范型判据,
为啥要执着的知道可控可观性呢?
还是从对角阵来看,有发散的极点,要想控制,那么输入一定要能影响这个部分。
控制的方式是状态反馈,知道是啥状态才好反馈回去。
可控可观性是个大前提,就和研究稳定程度一定要先稳定一样。
要控制系统,先得可控可观。
精确的描述可控可观
可控性有状态可控性和输出可控性。一般说的都是状态可控性,只看状态方程就行。前面引入的例子我们可以一眼看出可控,但是稍微复杂一点的,就得用数学方法了,
A system is completely controllable if there exists a control that can transfer any initial state to any desired location in a definite time.
对于一个离散系统 \(x(k+1) = Ax(k) + Bu(k)\)
令\(x(0) = 0\)迭代式
\[\begin{array} {l} \left\{ \begin{align} x(1) &= Ax(0) + Bu(0) = Bu(0)\\ x(2) &= Ax(1) + Bu(1) = ABu(0) + Bu(1)\\ x(3) &= Ax(2) + Bu(2) = A^2Bu(0) + ABu(1) + Bu(2)\\ \vdots \\ x(n) &= A^{n-1}Bu(0) + \dots + ABu(n-2) + Bu(n-1) \end{align} \right. \end{array}\]换个形式表达也就是
\[\boldsymbol{x}(n) = \left[\begin{array}{l} \boldsymbol{B} & \boldsymbol{AB} & \dots & \boldsymbol{A^{n-1}B} \end{array}\right] \left[\begin{array}{c} u(n-1) \\ u(n-2) \\ \vdots \\ u(0) \end{array}\right]\]可控性说的是任意状态向量\(\boldsymbol{x}(n)\)都找得到输入\(\boldsymbol{u}\),那么数学上就是说上面那个矩阵方程有解,那么就要求
\[rank \begin{bmatrix} \boldsymbol{B} & \boldsymbol{AB} & \dots & \boldsymbol{A^{n-1}B} \end{bmatrix} = n\]这个也是可控性的秩判据。
对于可控性,还有个很好玩的问题,在相平面上,可控是点对点的可控呢?还是说轨迹上的可控。只能说是点对点,而且还是理论上的可控,实际情况还有一些物理上的限制。
可控可观与传递函数矩阵的关系
单入单出
单入单出系统,可控、可观测的充要条件是:由动态方程导出的传递函数不存在零极点对消(不可约)。可控的充要条件是\((sI-A)^{-1}b\)无对消。可观的充要条件是\(c(sI-A)^{-1}\)
如果系统矩阵A又n个相异的特征值,那么可以对角化。
传递函数
\[G(s) = c(sI-A)^{-1}b\]多入多出系统
例题
举个例子
\[\dot{\hat{x}}=A\hat{x} + Bu\]其中
\[A = \left [ \begin{array} {cc:c:c:cc:c} -1 & 1 \\ 0 &-1 \\ \hdashline & &-1 \\ \hdashline & & &-1 \\ \hdashline & & & &2 &1 \\ & & & &0 &2 \\ \hdashline & & & & & &2 \\ \hdashline & & & & & & &5 \\ \end{array} \right ]\] \[B = \left [ \begin{array} {} 0 &0 &0 \\ 1 &0 &0 \\ \hdashline 0 &2 &0 \\ \hdashline 0 &0 &4 \\ \hdashline 0 &0 &0 \\ 1 &2 &0 \\ \hdashline 0 &3 &3 \\ \hdashline 8 &0 &0 \\ \end{array} \right ]\] \[C = \left [ \begin{array} {cc:c:c:cc:c} 2 & 0 &0 &0 &1 &0 &0 &0 \\ 0 & 0 &1 &0 &2 &4 &0 &7 \\ 0 & 0 &0 &3 &3 &0 &1 &0 \\ \end{array} \right ]\]每个约当块末行对应的B行不为全零行。
同一特征值的不同约旦快末行对应B的行向量无关。
记住算了。数学上的判断方法。就和一元二次方程有解公式一样,拿来就用。
